Багатофакторний кореляційно-регресійний аналіз

Кореляція, за допомогою якої вивчається вплив на величину результативної ознаки двох і більше факторних ознак, називається множинною. При вивченні множинної кореляції можна застосовувати як прямолінійні, так і криволінійні рівняння регресії.

Багатофакторні регресійні моделі дають змогу оцінювати вплив на досліджувану результативну ознаку кожного із факторів рівняння при фіксованому значенні (на середньому рівні) інших факторів. При цьому важливою умовою множинної кореляції є відсутність між факторами функціонального зв’язку.

Показниками щільності зв’язку при множинній кореляції використовують такі: парні, часткові і множинні (сукупні) коефіцієнти кореляції і множинний коефіцієнт детермінації.

Парні коефіцієнти кореляції використовують для вимірювання щільності зв’язку між двома досліджуваними ознаками без урахування їх взаємодії з іншими ознаками, включеними у кореляційну модель.

Часткові коефіцієнти кореляції характеризують щільність зв’язку результативної ознаки з однією факторною ознакою при умові, що інші факторні ознаки перебувають на постійному рівні. Парний коефіцієнт кореляції між результативною і факторною ознаками, як правило, не дорівнює відповідному частковому коефіцієнту.

Коефіцієнт множинної (сукупної) детермінації показує, яка частка варіації досліджуваного результативного показника зумовлена впливом факторів, включених у рівняння множинної регресії. Він може мати значення від О до +1. Чим ближчий коефіцієнт множинної детермінації до одиниці, тим більше варіація результативного показника характеризується впливом відібраних факторів.

Побудова множинної кореляційної моделі.

Лінійне рівняння регресії для множинної кореляційної моделі має вигляд:

.

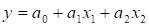
Для знаходження коефіцієнтів, і множинної кореляції розв’язуємо таку систему рівнянь, використавши дані таблиці 3.1.:

Розв’язавши дану систему рівнянь маємо:

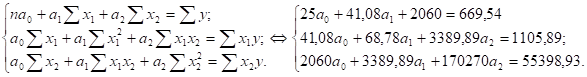
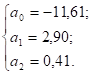
Отже, рівняння множинної регресії, яке характеризує залежність надою на корову від витрат кормів та виходу приплоду, матиме такий вигляд:

Знайдені коефіцієнти регресії показують, наскільки зміниться надій на корову при зміні відповідного фактора на одиницю при умові, що другий фактор, включений у рівняння, перебуває на середньому рівні. Так, показує, що при середньому обсязі витрат праці на 1 ц збільшення внесення органічних добрив на 1 т/га сприятиме зростанню урожайності картоплі на 5,9 ц/га. Збільшення обсягу витрат праці на 1 люд-год на 1 ц картоплі при середньому обсязі внесення органічних добрив сприятиме зниженню урожайності картоплі на 42,01 ц/га.

Обчислюємо:

1) парні коефіцієнти кореляції, , ,.

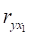
Виходячи з попередніх розрахунків, де та, та використовуючи дані з таблиці 3.1., маємо:

• а) ,
• б) ,
• в)

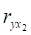
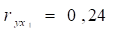
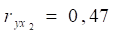
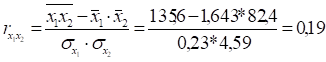
• 2) часткові коефіцієнти кореляції:
  • а)

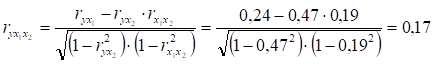
б).

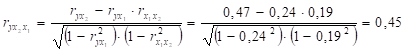
3) множинний коефіцієнт кореляції:

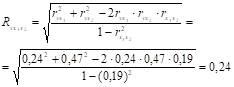
4) коефіцієнт множинної детермінації:

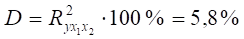
• 5) часткові коефіцієнти детермінації:
  • а)

б).

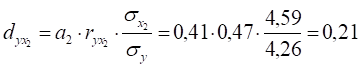
6) Перевірка суттєвості коефіцієнтів кореляції.

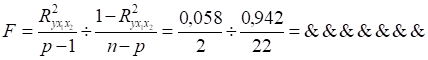
при та де — кількість одиниць спостереження; - кількість параметрів у рівнянні.

при ступенів свободи та дорівнює 3,44.

Отже, так як фактичне значення перевищує теоретичне, то можна сказати про існування істотного зв’язку між даними параметрами рівняння, тобто зв’язок між внесенням органічних добрив та витратами праці на 1 ц картоплі досить великий.