Тригонометричні рівняння з параметрами

Розглянемо рівняння.

F (х, у, …, z; б, в, …, г) =0 (F).

з невідомими х, у …, z і з параметрами б, в, …, г ;при всякій допустимій системі значень параметрів б₀, в₀, …, г₀ рівняння (F) звертається в рівняння.

F (х, у, …, z; б₀, в₀, …, г₀) =0 (F₀).

з невідомими х, у…, z, що не містить параметрів. Рівняння (Fo) має деяка цілком певна множина (може бути порожня) рішень.

Аналогічно розглядаються системи рівнянь, що містять параметри. Допустимими системами значень параметрів вважаються системи, допустимі для кожного рівняння окремо.

Означення. Вирішити рівняння (або систему), що містить параметри, це означає, для кожної допустимої системи значень параметрів знайти множину всіх вирішень даного рівняння (системи).

Поняття еквівалентності стосовно рівняння, що містить параметри, встановлюється таким чином.

Означення. Два рівняння (системи).

F (х, у, …, z; б, в, …, г) =0 (F),.

Ф (х, у, …, z; б, в, …, г) =0 (Ф) з невідомим х, у…, z і з параметрами б, в, …, г називаються еквівалентними, якщо для обох рівнянь (систем) множина допустимих систем значень параметрів одне і те ж і при всякій допустимій системі значень, параметрів обидва рівняння (системи рівнянь) еквівалентні.

Отже, еквівалентні рівняння при всякій допустимій системі значень параметрів мають одну і ту ж безліч рішень.

Перетворення рівняння, що змінює множину допустимих систем значень параметрів, приводить до рівняння, не еквівалентного даного рівняння.

Припустимо, що кожне з невідомих, таких, що містяться в рівнянні.

F (x, у, z; б, в, …, г)=0 (F).

задано у вигляді деякої функції від параметрів:

х = х (б, в,…, г); у = у (б, в, …, г);… z=z (б, в,… г). (Х).

Говорять, що система функцій (Х), заданих спільно, задовольняє рівнянню (F), якщо при підстановці цих функцій замість невідомих х, у…, z в рівняння (F) ліва його частина звертається в нуль тотожно при всіх допустимих значеннях параметрів:

F (x (б, в,… г), y (б, в,…, г),…, z (б, в,…, г)?0.

При всякій допустимій системі чисельних значень параметрів б=б₀, в=в₀, …, г= г₀ відповідні значення функцій (Х) утворюють вирішення рівняння.

F (х, у, …, z; б₀, в₀, …, г₀) =0.

Більшість тригонометричних рівнянь з параметрами зводяться до вирішення простих тригонометричних рівнянь трьох типів. При вирішенні таких рівнянь необхідно враховувати обмеженість тригонометричних функцій у = sin x і у = cos x. Розглянемо приклади.

Приклад 1. Вирішити рівняння: cos =2а.

Розв’язання: Оскільки Е (соs t)=[-1; 1], то маємо два випадки.

• 1. При |a| > 0,5 рівняння не має рішень.
• 2. При |a| ?0,5 маємо:
  • а) =arccos2a+2рn. Оскільки рівняння має рішення, якщо arccos2а+2рn?0, то n може приймати значення n=0, 1, 2, 3… Вирішенням рівняння є х = 1+(2рn+аrссоs2а)²
  • б) =-аrссоs2а+рn. Оскільки рівняння має рішення за умови, щоаrссоs2а+2рn>0, то n=1, 2, 3…, і вирішення рівняння. х=1+(2рn-arccos2a)² .

Відповідь: якщо |a| > 0,5, рішень немає;

якщо |a| ?0,5, х = 1+(2рn+аrссоs2а)²при n = 0, 1, 2… і х=1+(2рn-arccos2a)² при n N.

Приклад 2. Вирішити рівняння: tg ax² =.

Розв’язання:.

ах² = +рn, n Z.

Якщо коефіцієнт при невідомому залежить від параметра, то з’являється особливе значення параметра. В даному випадку:

1. Якщо а=0, то рівняння не має рішень.

2. Якщо, а 0, то х2 =, n Z.

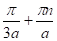
Рівняння має рішення, якщо ?0. З’ясуємо, при яких значеннях n.

і а виконується ця умова:

?0.

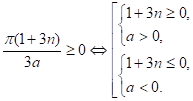
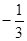
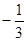
звідки n? і а > 0 або n? і а < 0.

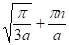
Отже, рівняння має вирішення х = ±, якщо.

• 1) а > 0 і n = 1,2,3. або
• 2) а < 0 і n Z.

Відповідь: при, а = 0 рішень немає;

при, а > 0 і n = 1,2,3. або, а < 0 і n Z х = ± .

Приклад 3. Вирішити рівняння: а sin bx = 1.

Розв’язання: Особливе значення параметра, а: а = 0.

• 1. При, а = 0 рішень немає.
• 2. При, а 0 sin bx =. Маємо 2 випадки:
• 2.1. Якщо > 1, то рішень немає.
• 2.2. Якщо? 1, то особливе значення b = 0:
• 2.2.1. Якщо b = 0, то рішень немає.
• 2.2.2. Якщо b 0, то х =

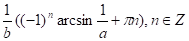
Відповідь: при, а = 0 або > 1 і а 0 або, а 0 b = 0 рішень немає;

при, а 0 і ?1 і b 0 х =.