Визначення передаточних функцій елементів САК

У ТАК елементи автоматичних систем з точки зору їх динамічних властивостей зображують за допомогою динамічних ланок. Під динамічною ланкою розуміють математичну модель штучно виділеної частини системи, яка характеризується певним алгоритмом передачі сигналу зі входу ланки на її вихід (мал. 1).

автоматичний керування передаточний ланка.

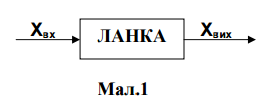
Вхідна x_вх. і вихідна x_вих. величини відповідають фізичним величинам, що зображують дію попередньої ланки на дану ланку (x_вх.) і дію даної ланки на наступну (x_вих.). Рівняння динаміки елементу системи (ланки) визначає залежність його вихідної величини x_вх. від вхідної величини x_вих. і, як правило, подається в диференціальній формі. Ланка САК може являти собою технічний пристрій будь-якої фізичної природи, конструкції та призначення. Тому складання рівняння динаміки конкретної ланки є предметом відповідної галузі технічних наук (механіки, електротехніки, теплотехніки і т.ін.), до яких і слід звертатися кожного разу.

Якщо задано диференціальне рівняння, що описує залежність вихідної величини елементу від вхідної, передаточна функція ланки W(p)визначається за допомогою перетворення Лапласа за нульових початкових умов.

Розглянемо визначення передаточної функції ланки на прикладі диференціального рівняння електричного RL - ланцюжка (мал. 2):

Запишемо початкове диференціальне рівняння в операційній формі (тобто в зображеннях за Лапласом), використовуючи такі теореми перетворення Лапласа:

1. Теорема про додавання (лінійність перетворення)

L{a₁ f₁(t) + a₂ f₂(t)}= a₁L{f₁(t)}+ a₂L{f₂(t)}.

2. Теорема про інтегрування.

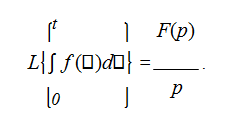
3. Теорема про диференціювання (за нульових початкових умов).

L{f ⁽ⁿ⁾(t)}= pⁿF(p) _.

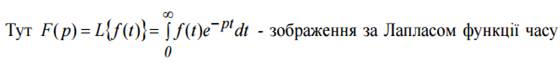
f (t) ; p = у + jщ - комплексна змінна перетворення Лапласа.

Відповідно до наведених теорем, функції часу, що входять до диференціального рівняння, замінюються на їх зображення за Лапласом, а операції диференціювання (інтегрування) у випадку нульових початкових умов — множенням (діленням) на комплексну змінну p зображень функцій, від яких береться похідна (інтеграл).

Диференціальне рівняння (1) в операційній формі для випадку нульових початкових умов має вигляд:

(Tp + 1)Uвих(p) = KUвх(p) . (2).

Передаточна функція ланки (системи) W(p) являє собою відношення зображень за Лапласом вихідної X_вих(p) і вхідної X_вх(p) величин за нульових початкових умов:

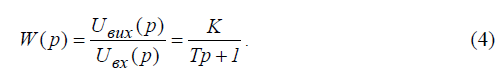
тобто передаточна функція може бути визначена із рівняння ланки, записаного в операційній формі, і для рівняння (2) має вигляд:

Якщо елемент системи має дві вхідних величини, необхідно визначити дві передаточні функції (за кожним входом). Нехай диференціальне рівняння елемента:

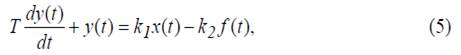
де у (t) — вихідна величина; x (t), f (t) — відповідно регулююче і збурююче діяння (знак «-» показує, що за зростання f (t) відбувається зменшення y (t)).

Покладаємо, у = у_х + у_f тоді рівняння (5) розбивається на два рівняння:

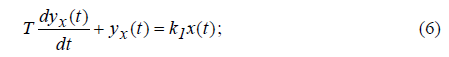
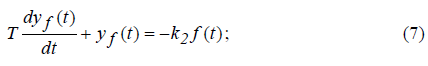
яким відповідають дві передаточні функції:

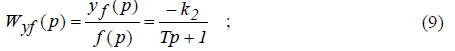
де уx — вихідна величина, що зумовлена регулюючим діянням х за f = 0 ; уf — вихідна величина, що зумовлена збурюючим діянням f за x = 0 .