Алгебраїчні рівняння.
Алгебраїчні рівняння

Визначення. Рівнянням називається рівність, який містить перемінні величини і виконується лише при деяких значеннях цим перемінних. Розв’яжемо рівняння (1) означає знайти всі його корні і доказати відсутність інших корнів, крім найдених. Два рівняння, називається еквівалентним або рівносильним, якщо множина їх рішення співпадає. При зведенні в квадрат обох частин рівняння (3) може приходити до… Читати ще >
Алгебраїчні рівняння. Алгебраїчні рівняння (реферат, курсова, диплом, контрольна)
Загальні відомості про рівняння
Визначення. Рівнянням називається рівність, який містить перемінні величини і виконується лише при деяких значеннях цим перемінних.
Нехай — функція, яка визначена при дійсних значеннях і приймає лише дійсні значення. Якщо, то число називається нулем функції або коренем рівняння.
. (1).
Розв’яжемо рівняння (1) означає знайти всі його корні і доказати відсутність інших корнів, крім найдених.
Два рівняння, називається еквівалентним або рівносильним, якщо множина їх рішення співпадає.
Процес рішення рівняння (1) — це перетворення рівняння (1) до виду, який позволяє легко знайти його корні. Під година перетворення рівняння (1) область визначення рівняння може змінюватися і при цьому можливо поява сторонніх корнів або втрата корнів.
Приклад. При розв’язанні ірраціонального рівняння.
(2).
зводимо дві частини рівняння в квадрат.
, .
При зведенні рівняння в квадрат область припустимих значень розширюється і появляються сторонній корінь, який являється коренем рівняння.
. (3).
При зведенні в квадрат обох частин рівняння (3) може приходити до рівняння .
Приклад. Розв’яжемо алгебраїчне рівняння.
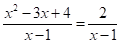
.
Прирівнюючи чисельники, приходимо до рівняння.
.
Розв’язок не являється розв’язком вихідного рівняння.