Методика вивчення теми «Звичайні та десяткові дроби та дії над ними»

Введение

дробных чисел в школьном курсе связывается с необходимостью более точного измерения величин, с делением чисел. В связи с этим целесообразно познакомить учащихся с возникновением дробных чисел в процессе практической деятельности человека, а именно в процессе измерения. Краткая историческая справка поможет учащимся лучше овладеть данным материалом. Согласно программе и учебнику по математике формирование понятий дроби начинается с умения получать доли при делении какой-либо величины на несколько равных частей.

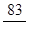
Учащимся сообщается, что для выражения одной или нескольких долей предмета нужны новые числа, а именно дроби. Далее приводятся примеры обыкновенных дробей и даётся форма записи обыкновенной дроби, проводится обучение чтению. Учащиеся должны помнить: числитель дроби — количественное числительное женского рода (одна, две и т. д.), а знаменатель — порядковое числительное (седьмая, сотая, двести тридцатая и т. д.). Например, — одна пятая; — две шестых; — семь десятых; — восемьдесят три сто пятьдесят вторых. В процессе работы над закреплением понятия дроби необходимо познакомить учащихся с происхождением слова «дробь», ввести термины «числитель», «знаменатель». После рассматриваются признаки дробей, затем приведение дробей к общему знаменателю (замена дробей равными им дробями, имеющими одинаковые знаменатели).

Объяснение материала сложения дробей с одинаковыми знаменателями. Для этого нужно начертить на доске квадрат и разделить его на 9 равных частей (долей), для того чтобы учащиеся убедились, что каждая часть (доля) может выражаться дробью. Предложить учащимся закрасить две такие части одним цветом, три части — другим цветом и поставить перед ними вопрос: «Сколько всего закрашенных частей». Ученики ответят, что закрашено 5 частей. Если записать сказанное в виде дроби, то получится.

;

при записи с помощью букв:

.

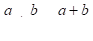
После этого учащиеся сами могут сформулировать правило сложения дробей с одинаковыми знаменателями.

Далее можно переходить к правилу сложения дробей с разными знаменателями. Чтобы сложить дроби с разными знаменателями, нужно сначала привести их к наименьшему общему знаменателю, затем, используя правило сложения дробей с одинаковыми знаменателями, продолжать выполнить сложение.

Например, чтобы найти сумму дробей 5/7+¾, нужно найти наименьшее общее кратное знаменателей данных дробей. НОК (7,4)=28. Следовательно, наибольшим общим знаменателем дробей 5/7 и ¾ является число 28. Дополнительные множители 28:7=4 и 28:4=7.

Приведем дроби к наименьшему общему знаменателю.

.

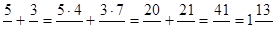
Выполняемость переместительного и сочетательного свойств при сложении дробей учащиеся должны проверить сами. Тогда усвоение нового материала будет более результативным.

Например,.

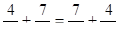
— переместительное свойство.

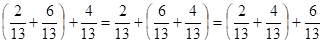
— сочетательное свойство.

Поскольку целые части смешанных чисел являются натуральными числами, сложение смешанных чисел состоит из сложения натуральных чисел и сложения дробей с разными знаменателями. Кроме того, при сложении смешанных чисел, складывая целые и дробные части отдельно, применяют переместительное и сочетательное свойства сложения.

Например,.

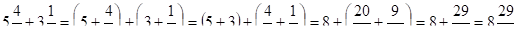
После того, как учащиеся овладеют навыками сложений смешанных чисел, задавая наводящие вопросы, можно предложить им сформулировать правило сложения смешанных чисел.

Учащиеся, используя пример 12 5/7+9/14, приходят к выводу о том, что сумма смешанного числа и правильной дроби является смешанным числом.

Например,.

.

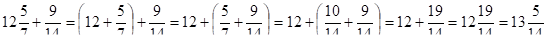
Учащиеся могут приобрести навыки сложения натурального и смешанного чисел при выполнении таких примеров:

.

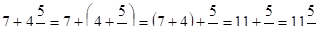
Чтобы закрепить навыки, приобретенные учащимися при изучении основных положений данной темы, учитель может провести фронтальный опрос, предложить повторить правила сложения различных смешанных чисел.

Вычитание дробей с одинаковыми знаменателями объясняется использованием отрезков различной длины.

Например: длина отрезка АВ равна, а длина отрезка АС-. Найдите длину отрезка СВ.

Решение: СВ = АВ-АС, тогда СВ=7/8−3/8=4/8=½.

При написании формул с помощью букв вычитание дробей с одинаковыми знаменателями, выглядит так:

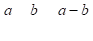
где .

Далее следует объяснение вычитания дробей с разными знаменателями. Для вычитания дробей с разными знаменателями нужно привести к наименьшему общему знаменателю данные дроби, записав их с одинаковыми знаменателями.

Например,.

.

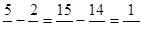
После выполнения учащимися нескольких примеров и овладения навыками таких вычислений можно задать наводящие вопросы, для того чтобы учащиеся сформулировали правило вычитания дробей с разными знаменателями.

Выполнение умножения обыкновенных дробей обычно рассматривается на примере нахождения площади прямоугольника, вырезанного из квадрата. Чтобы вырезать прямоугольник длиной 4/5дм, шириной — 2/3 дм из квадрата, длина которого равна 1 дм, нужно, разделив его на 15 частей, вырезать прямоугольник, длина которого состоит из 4 частей, ширина из 2 частей. Тогда учащиеся убеждаются в том, что вырезанный прямоугольник состоит из 8 частей и что площадь одной части равна 1/15 дм². Отсюда видно, что площадь полученного прямоугольника равна 8/15 дм². Числитель дроби представляет собой произведение числителей умножаемых дробей, а знаменатель — произведение знаменателей умножаемых дробей. После этого, задавая дополнительные наводящие вопросы можно помочь учащимся самостоятельно сформулировать правило умножения дробей.

Например,.

• 1. На сколько частей разделили квадрат?
• 2. Из скольких частей состоит прямоугольник?
• 3. Как получили числитель дроби произведения?
• 4. Как получили знаменатель дроби произведения?

Ответив на эти вопросы, учащиеся смогут самостоятельно сформулировать правило умножения дробей.

Учитель обязательно должен дать правило умножения дробей, произнеся определение приподнятым тоном, затем показать, как это правило записывается с помощью букв.

.

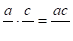
Следует напомнить учащимся о том, что, прежде, чей приступить к умножению обыкновенных дробей, нужно сократить дроби и записать их в виде несократимых дробей, затем выполнить умножение.

Например,.

.

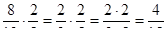
В учебнике особое внимание уделено умножению натуральных чисел на обыкновенные дроби. Любое натуральное число можно представить в виде неправильной дроби со знаменателем 1. При умножении его на 1 снова получается само это число. Поэтому при умножении натурального числа на дробь нет необходимости в представлении натурального числа в виде неправильной дроби со знаменателем 1. После объяснения этого учащимся нужно сформулировать правило: чтобы умножить натуральное число на дробь, надо числитель дроби умножить на это число, а знаменатель оставить без изменения.

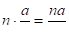
или .

Например,.

.

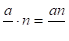
При объяснении учащимся правила умножения смешанных чисел следует сказать о том, что сначала необходимо представить их в виде неправильных дробей, только затем приступить к умножению их, применяя правило умножения дробей.

Например,.

.

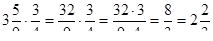
В учебнике деление обыкновенных дробей объясняется на примере решения уравнения, в котором один из множителей дан в виде неизвестной дроби.

В начале, когда учащиеся только приступают к изучению деления дробей, они могут записать последовательно все производимые ими операции. Когда учащиеся овладеют навыками выполнения деления обыкновенных дробей, учитель может требовать от них сокращенную запись деления дробей.

Это, во-первых, позволяет экономить время, во-вторых, способствует повышению скорости мышления учащихся, прививает навыки логического мышления. Такой дидактический прием лишен наглядности, однако он постоянно активизируя познавательную деятельность учащихся, имеет прогрессивное значение.

Десятичные дроби не являются новыми числами по сравнению с обыкновенными дробями. Они представляют лишь другую запись ранее известных обыкновенных дробей со знаменателями 10, 100, 1000 и т. д. В математических вычислениях и практических расчетах более удобными являются десятичные дроби. Основные цели изучения темы «Десятичные дроби» — сформировать навыки чтения, записи, сравнения и вычислений с десятичными дробями, их округления. При изучении темы рассматриваются возможности записи чисел в различных эквивалентных формах. Для этой цели предлагаются задания на запись натуральных чисел в виде обыкновенной и десятичной дроби, на запись десятичных дробей в виде обыкновенных, на выбор обыкновенных дробей, которые можно записать в виде десятичных, пользуясь основным свойством дроби.

Поскольку десятичные дроби являются числами, записанными в десятичной системе, сложение десятичных дробей выполняют так же, как и сложение натуральных чисел. Запись слагаемых одно под другим в столбик так, чтобы запятые оказались друг под другом, является основным условием сложения десятичных дробей. Об этом следует сказать учащимся. При такой записи слагаемых одноименные разряды указываются друг под другом, что позволяет произвести сложения десятичных дробей. После этого десятичные дроби складываем так же, как складывали натуральные числа. В полученном результате запятую ставим под запятой в данных дробях.

При использовании этого способа сложения нужно, превратив слагаемые (десятичные дроби в обыкновенные), проверить полученную сумму сложением обыкновенных дробей.

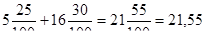
При сложении десятичных дробей выполняются переместительное и сочетательное свойства сложения. Использование этих свойств облегчает выполнение сложения дробей.

Например,.

• (2,3+5,81)+6,7=(2,3+6,7)+5,81=9+5,81=14,81
• — здесь использовано переместительное свойство сложения.

В задании для предварительной подготовки учащихся к новой теме уменьшаемое и вычитаемое, данные в виде десятичных дробей, записаны так, чтобы одноименные разряды оказались друг под другом. Учащиеся выполняют вычитание десятичных дробей по разрядам, начиная с наименьшего разряда.

• 3,7−1,2=2,5
• 7,21−1,5=5,71
• 25−2,64=22,36.

При вычитании десятичных дробей, точно так же как и в случае сложения десятичных дробей, уменьшаемые и вычитаемые дроби записывают так, чтобы запятые находились друг под другом, затем уравнивают число десятичных знаков них, выполняют вычитание, начиная с наименьшего разряда.

Например,.

• 18,45−9,76=8,69
• 18,45
• — 9,76
• 8,69

Проверка в виде обыкновенных дробей.

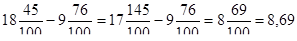
Если уменьшаемое представляет собой натуральное число, то, поставив после него запятую, к нему приписывают нужное число нулей и выполняют вычитание.

Тему умножения десятичных дробей начинается с умножения десятичной дроби на натуральное число.

Умножение десятичной дроби на натуральное число можно заменить суммой слагаемых, каждое из которых равно этой десятичной дроби, а количество слагаемых — данному натуральному числу.

Например,.

.

При умножении десятичных дробей на разрядные единицы 10,100, 1000 и т. д. путем логического синтеза учащиеся приходят к следующему выводу. Чтобы умножить десятичную дробь на 10,100,1000 и т. д.

разрядные единицы, надо запятую в этой дроби перенести настолько знаков вправо, сколько нулей в разрядной единице.

После объяснения материала нужно задать вопросы по основным моментам новой темы. Это способствует закреплению и обобщению знаний учащихся.

При выполнении умножения десятичных дробей нужно обратить внимание учащихся на то, что сумма десятичных знаков множителей равна количеству десятичных знаков произведения. После этого учащиеся смогут путем логического синтеза самостоятельно сформулировать правило умножения десятичных дробей. Затем можно приступить к проверке уровня усвоения учащимися новой темы.

При делении десятичной дроби на натуральное число сначала делят целую часть десятичной дроби на натуральное число, ставят запятую в частном после окончания деления целой части (для того, чтобы отделить целую часть частного от его дробной части), затем делят дробную часть.

Например, .

Правильность полученного результата учащиеся могут проверить умножением частного на делитель: .

Например,. Решая пример, сформулируем правило деления десятичной дроби на натуральное число:

• 1. не обращая внимания на запятую, нужно разделить дробь на это число;
• 2. поставить запятую в частном, когда закончится деление целой части, продолжить деление, пока в остатке не останется нуль.

Если целая часть делимого меньше делителя, то частное начинается с нуля.

Например, 1,2:5=0,24.

Чтобы разделить десятичную дробь на разрядные единицы 10, 100, 1000 и т. д., надо перенести запятую десятичной дроби на столько знаков влево, сколько нулей в разрядных единицах. Деление десятичных дробей на разрядные единицы 10, 100, 1000 и умножение десятичных дробей на разрядные доли 0,1, 0,01, 0,001 и т. д. дают одинаковый результат.

Например, 4,29:10=0,429.

Важным элементом методики изучения чисел является убеждение учащихся в целесообразности введения новых чисел. Обыкновенные дроби использовались для записи долей. Возможность записать доли с помощью обыкновенных дробей является одним из приемов убеждения учащихся в полезности таких дробей. Помимо этого существуют еще два других приема, показывающих необходимость введения дробных чисел. Мотивировать введение дробных чисел можно также тем, что с их помощью операция деления натуральных чисел делается всегда выполнимой. Как известно, в множестве натуральных чисел число 2 не делится на число 3. дополним это множество дробями и вновь рассмотрим деление числа 2 на 3. Третий прием мотивации введения дробных чисел связывается с задачей измерения величин. Пусть, например, требуется измерить длину отрезка в сантиметрах.