Методи утворення від`ємних температур. 
Активні середовища квантових приладів

У оптичних квантових генераторах, працюючих на твердих кристалічних тілах, перехід системи до збудженого стану можна здійснити за допомогою зовнішнього електромагнітного поля. При такому засобі досягнення інверсної населеності використання тільки двох рівнів неможливо, оскільки імовірності переходів однакові. Тому при опроміненні можна тільки зменшити різницю () в порівнянні з рівноважною, але не зробити її від`ємною і, отже, не можна отримати від`ємний коефіцієнт поглинання.

Малюнок 3.1 — Переходи до трирівневої системи.

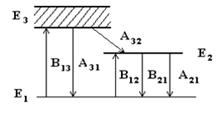
Розглянемо систему з трьома енергетичними рівнями і () з населеністю і відповідністю (мал. 3.1). У рівноважному стані в кристалі майже всі атоми знаходяться на нижньому основному енергетичному рівні, тобто і.

Під дією випромінювання від зовнішнього джерела системою поглинається енергія, відповідна до частоти широкої смуги рівня 3. Смугу поглинання рівня 3 прагнуть підібрати по можливості більш ширшою. Це збільшує К.К.Д. квантового генератору. Газорозрядні лампи або інші джерела енергії, як правило, мають широкий спектр випромінювання. Тому, чим ширше рівень 3, тим більша енергя накачування, що використовується на збудження квантової системи. Звичайне випромінювання, що викликає перехід атомів на збуджені рівні, називають випромінюванням накачування, а сам процес створення інверсної населеності за допомогою зовнішнього електромагнітного випромінювання називається накачуванням.

При виборі системи з трьома рівнями звичайно прагнуть дотриматись таких умов.

Імовірність невипромінюваного переходу повинна бути значно більшою, ніж, тобто або (3.1).

За цієї умови протягом години велика частина збуджених атомів перейде на рівень 2.

Імовірність спонтанного переходу повинна бути значно меншою ніж імовірність, тобто.

або (3.2).

Це означає, що рівень 2 повинен бути значно стійкішим (метастабільним) в порівнянні з рівнем 3, що забезпечує накопичення збуджених атомів на рівні 2. При досить високій потужності накачування може бути досягнута інверсія населеності між рівнем 2 і основним рівнем, але оскільки час життя рівня 3 малий, то збуджені атоми не затримуються на ньому і невипромінювано переходять на триваліший рівень 2, створюючи інверсну населеність цього рівня відносно до рівня 1. Час життя рівня 2 повинен бути досить великим, щоб нагромадити на ньому енергію, необхідну для генерації. Наприклад, для рубіна с., а с., тобто час життя рівня 2 в рубіні в разів більший часу життя рівня 3.

Враховуючи зміни населеності всіх трьох рівнів внаслідок різних переходів, кінетичні рівняння переходів в квантовій трирівневої системи можна записати в такому вигляді:

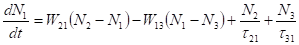
(3.3).

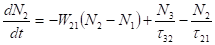
(3.4).

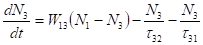
. (3.5).

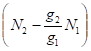
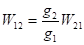
Ці рівняння записані в спрощеній формі, оскільки в них не враховане виродження рівнів. Якщо енергетичні рівні характеризуються деякими мірами виродження, то необхідно замінити на і згідно з першим співвідношенням Ейнштейна, а не .

Враховуючи особливості конкретної системи, ці рівняння можна спростити.

Одне з них можна виключити, замінивши простішим співвідношенням.

(3.6).

де — загальна кількість атомів активатора в 1 смі.

Якщо далі передбачити, що накопичення на рівні 3 не відбувається, як у випадку рубінового ОКГ, тобто.

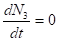
і, (3.7).

те рівняння (3.5) матиме вигляд.

а сама система перетвориться в дворівневу, оскільки.

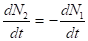
Враховуючи ці допущення, перетворюємо рівняння (3.3) і (3.5), що матимуть такий вигляд:

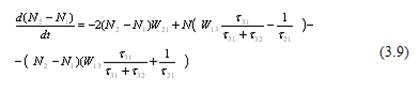
Оскільки в рубіні швидкість переходу з рівня 3 на метастабільний рівень 2 значно більше швидкості переходу з рівня 3 на рівень 1, тобто, то рівняння (3.9) приймає вигляд.

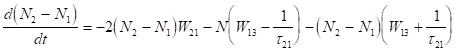
. (3.10).

У стаціонарному режимі, тобто при, маємо.

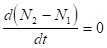
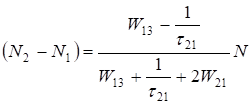
. (3.11).

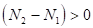
З цього рівняння видно, що необхідна умова генерації може бути виконана тільки при таких потужностях накачування, коли, тобто.

(3.12).

Величина ймовірностей переходів атомів з рівня 1 на рівень 3 внаслідок накачування визначається таким чином.

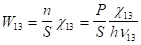
(3.13).

де n — кількість фотонів, що падають нормально поверхні кристала S в одиницю часу; - ефективний перетин поглинання для переходу атома з рівня 1 на рівень 3 при впливі квантів; Р — потужність накачування в смузі частот поглинання активної речовини.

З урахуванням значення (3.13) і порогової умови накачування (3.12) можна отримати вираз для порогового значення потужності випромінювання накачування:

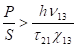
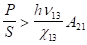
або. (3.14).

Для рубіна, наприклад, при значеннях с.,, Дж порогова потужність накачування повинна складати. Насправді, порогова потужність накачування значно більше цієї величини внаслідок різних втрат в оптичному резонаторі.

Згідно з виразами (3.11), (3.12) і (3.14) ймовірність генерації та порогова потужність накачування істотно залежать від ймовірності спонтанного переходу з метастабільного рівня на основний рівень 1.

Цей перехід зумовлює флуоресценцію збудженого кристала рубіна, тобто втрати на некогерентне випромінювання. Частка флуоресценції у випромінюванні рубінового ОКГ досить велика. Це призводить до того, що енергія, необхідна для збудження половини всіх атомів з основного стану, не переходить в когерентне випромінювання.

Зручнішою з енергетичної точки зору є система з чотирма рівнями (мал. 3.2). В цій системі вимушене випромінювання відбувається при переході активних атомів між рівнями, з яких рівень 2 розташований вище основного рівня 1. Різниця повинна бути значно більшою кванта теплових коливань kT, щоб зробити неможливим перехід атомів за рахунок теплових коливань з основного рівня 1 на рівень 2, тобто повинне бути.

. (3.15).

Якщо ця умова не виконана і.

(3.16).

то система стає трирівневою, оскільки рівень 2 фактично зливається з рівнем 1.

Практично систему можна вважати чотирирівневою, якщо, і трирівневою, якщо справедливий вираз (3.16).

Якщо умова (3.15) виконана, то при термодинамічній рівновазі населеність рівня 2 дуже мала. Оскільки рівень 2 завжди не заповнений, то для створення інверсної населеності досить перевести з основного стану в стан 3 хоч би декілька атомів. Тому, для збудження чотирирівневих генераторів потрібна значно менша витрата енергії, ніж для трирівневих.

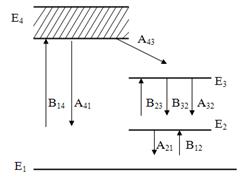
Малюнок 3.2 — Переходи до чотирирівневої системи.

Вперше чотирирівневий ОКГ був здійснений Сорокіним та Стівенсоном (США), які використали для цього кристали флюорита () з або або (при концентрації активних атомів).

Найтиповішою чотирирівневою активною речовиною є скло з домішками тривалентних іонів неодима. Умова (3.15) у скла з неодимом і у флюорита з ураном виконується при температурі. Тому квантові генератори на цих речовинах добре працюють при кімнатній температурі, не вимагаючи спеціального охолодження Рівень 2 у них знаходиться приблизно на вище основного рівня 1. В кристалі рівень 2 знаходиться на відстані над основним рівнем 1. Тому при кімнатній температурі таке середовище нічим не відрізняється від трирівневої системи і працює як чотирирівнева лише при температурах нижче.

Крім цієї умови при виборі чотирирівневої системи прагнуть виконати всі умови, розглянуті в попередньому розділі для трирівневих систем.

Кінетичні рівняння населеності рівнів в чотирирівневій системі можна записати в такому вигляді:

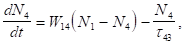
(3.17).

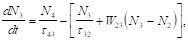
(3.18).

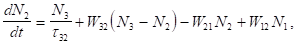
(3.19).

(3.20).

Так само як у разі трирівневої системи, будемо вважати, що накопичення атомів на рівні 4 не відбувається, тобто.

і (3.21).

що справедливо при.

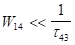
тобто або (3.22).

Ця умова звичайно завжди виконується так само, як і для рівня 2, де також не повинне відбуватися накопичення атомів, тобто.

або (3.23).

Таким чином, чотирирівнева система також зводиться до дворівневої, і рівняння перетворюються у вираз.

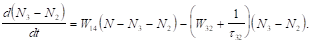
(3.24).

У стаціонарному режимі.

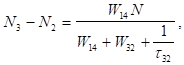
(3.25).

тобто необхідна умова генерації в цьому випадку не має того обмеження, яке накладає флюоресценція в трирівневій системі. Тому у вираженні порогової потужності накачування, для чотирирівневої системи множник, що характеризує ймовірність спонтанного переходу буде відсутнім. Отже, чотирирівнева система може працювати в режимі генерації при значно менших потужностях накачування [3].

Задача 1. Оцінити мінімальну потужність лампи-спалаху, необхідну для накачування твердотільного лазера. Кількістьактивних часток в кристалі част/смі, об'єм кристала V = 10 смі.

Час життя часток на верхньому робочому рівні с. Середина смуги, в якій відбувається основне поглинання випромінювання джерела накачування, Гц. Прийняти к.к.д. лампи накачування 100%.

Інверсія настає, якщо на верхньому робочому рівні знаходиться більше ніж половина активних часток.

Задача 2. Розглянути накачування лазерного кристала джерелом інтенсивністю в одиничному інтервалі довжин хвиль. Кристал (мал. 3.3), виконаний у вигляді прямокутного паралелепіпеда довжиною L з квадратним перетином (бік квадрата а). Дзеркала нанесені прямо на грані кристала (штриховка).

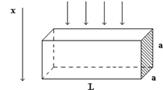
Малюнок 3.3 — Геометрія накачування лазерного кристала Випромінювання джерела накачування падає перпендикулярно до грані кристала в напрямі осі x. Коефіцієнт поглинання випромінювання в кристалі, квантова ефективність.Джерело накачування вважати досить вузькосмужним, тобто в межах ширини спектру джерела величини, і можна вважати постійними:

;;.

• 1. Оцінити порогову потужність джерела накачування, вважаючи, що поглинання в кристалі невелике і не впливає на інтенсивність випромінювання, яке проходить крізь кристал .
• 2. Врахувавши зміну інтенсивності сигналу накачування за рахунок поглинання в кристалі, визначити граничну товщину кристала, для якої накачування ще ефективне. У цьому випадку вважати, що

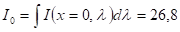
Вт/см2.

Крім того, при оцінюванні використати наступні дані, см-3, см-1, мкм,. Ширина лінії люмінісценції (при Т = 290К) см-1, довжина паралелепіпеда L = 1,2 см, а бік квадрату, а = 0,1 см, коефіцієнт відображення дзеркал, довжина хвилі випромінювання мкм.

Розв`язання.

Оцінимо потужність джерела накачування, що поглинається в одиниці об'єму кристала.

За рахунок поглинання в кристалі інтенсивність падаючого на грань кристала випромінювання джерела накачування зменшується згідно із законом.

(3.26).

Зміну інтенсивності на елементі шляху в площині кристала рівно [використовуючи рівняння (3.25)].

Таким чином, потужність, що поглинається в одиниці об'єму та інтервалі довжин хвиль від до, дорівнює.

З цієї кількості тількия частина йде на створення інверсної населеності, тобто корисна потужність Енергія поглиненого фотона Вважаючи, що один поглинений фотон призводить до появи однієї збудженої частки на верхньому робочому рівні, отримуємо, що число часток, які збуджуються в одиниці об'єму в одиницю часу за рахунок поглинання випромінювання у всій ширині джерела, дорівнює.

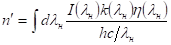
Оскільки,, в межах спектру випромінювання джерела мало змінюються, виносимо їх з-під знаку інтеграла, отримуючи.

.

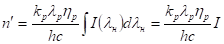
Де.

— інтегральна за спектром інтенсивність джерела накачування.

.

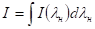
Кількість часток в одиниці об'єму, що йдуть з рівня в одиницю часу за рахунок спонтанних переходів на поріг генерації, дорівнює (розглядається порогове значення накачування).

Очевидно, повинно виконуватися рівняння і, отже,.

.

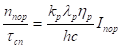
тобто порогова інтенсивність.

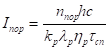
. (3.27).

При відсутності виродження для лоренцевої форми лінії.

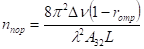
. (3.28).

Підставляючи (3.27) в (3.26) і враховуючи, що, а довжина хвилі випромінювання в кристалі пов’язана з довжиною хвилі випромінювання у вакуумі () співвідношенням, маємо.

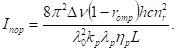
(3.29).

Для початкових даних задачі це дає Вт/см². Поверхня кристала, на яку падає потік см², тобто потужність падаючого на кристал випромінювання Вт.

Гранична товщина кристала визначається з умови, що при проникненні в глибину кристала на відстань, а інтенсивність падає остільки, що інверсна населеність стає менше порогової.

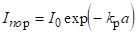
Якщо — початкова інтенсивність, то, а визначиться з умови, де знаходять по формулі (3.28). Таким чином,.

.

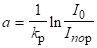
Для Вт/см², Вт/см², використовуючи початкові дані, отримуємо см.

Задача 3. Приписати значення від`ємної температури системі двох енергетичних рівнів. Населеність верхнього та нижнього рівнів дорівнює відповідно см3 і см³. Кратністьь виродження верхнього рівня 2, нижній рівень не виражений.

Чи можливе в системі, що розглядається, посилення? Поглинання?

Задача 4. Отримати умову інверсної населеності для обертальних-коливальних рівнів (обертально-коливальна інверсія) між рівнями, і, лінійної молекули без центру інверсій.

Вважати, що розподіл по обертальних рівнях дуже швидко встановлюється і після цього може бути представлений у вигляді.

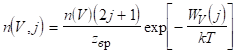
. (3.30).

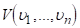
Обертально-коливальний рівень задається набором коливальних чисел та обертальним числом.

Енергія.

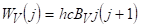
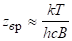
а, де Ткінетична температура газу, що визначається температурою обертальних і поступальних заходів свободи.

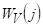
Визначити мінімальне значення числа j, для якого виконується умова інверсної населеності для обертальних рівнів молекули HF. Для оцінок прийняти частоту смуги см-1, см-1, см-1,. У вираженні для на відміну від попередньої задачі міститься з, оскільки задається в см-1.

Задача 5. На малюнку (3.4) показана чотирівнева система. Накачування йде з нижнього рівня 1 на самий верхній рівень 4. Інверсная населеність утворюється між середніми рівнями 3, 2.

Імовірність переходів з рівня 4 на рівень 3 і з рівня 2 на рівень 1 досить велика, так що рівні 4 і 2 можна завжди вважати порожніми.

Кінетичні рівняння для такої системи звичайно записуються у вигляді:

;

.

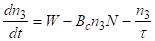
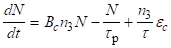
де W — число часток, що попадають на рівень 3 за рахунок накачування в одиницю часу; n3 — число часток на рівні 3 (нагадаємо, що число часток на рівні 2 дорівнює n2=0); Bc константа, що залежить від частоти; N — число фотонів в типі коливань резонатора лазера; - час спонтанного випромінювання; - час життя фотонів в резонаторі; - ймовірність того, що фотони, які утворюються внаслідок спонтанного розпаду, попадають в тип коливань, що розглядається.

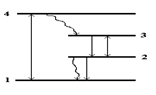
Малюнок 3.4 — Чотирирівнева система. Накачування відбувається з рівня 1 на рівень 4. Робочий перехід Прямими стрілками показані випромінювані переходи, хвилястими невипромінювані.

1) Визначити Bc і і показати, що, тобто показати, що кінетичне рівняння для числа фотонів можна записати у вигляді.

.

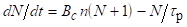
2) Написати явний вигляд виразів Bc і для лоренцової форми лінії люмінесценції активної речовини.

Задача 6. Визначити порогову населеність для початку генерації на R1 лінії рубіна.

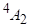
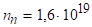
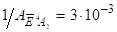
Діаграма енергетичних рівнів іона Cr3+ в рубіні показана на малюнку (3.5). Рівень двократно, рівень чотирикратно виражені. Щильність активних часток для стандартного рубінового кристала см-1, температура кристала Т = 300 К, дзеркала нанесені прямо на грані кристала і мають коефіцієнт відображення, довжина кристала L = 5 см, напівширина лінії люмінесценції на напіввисоті см-1, час спонтанного випромінювання переходу, с, показник заломлення кристала, довжина хвилі випромінювання у вакуумі см.

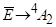
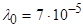
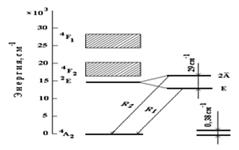
Малюнок 3.5 — Діаграма енергетичних рівнів іона в рубіні.

На малюнку в сильно збільшеному масштабі показано, що рівень розщеплений на два з відстанню 0,38 см -1між ними.

Примітка. При розрахунку необхідно враховувати також рівень, який лежить вище рівня на 29 см-1. Між рівнями і теплова рівновага встановлюється досить швидко, так що населеність цих рівнів підкоряється розподілу Больцмана.

Задача 7. Користуючись результатами попередньої задачі, приписати робочим рівням R1 — лінії рубіна значення абсолютної негативної температури на порозі генерації.

Задача 8. Знайти стаціонарне рішення кінетичних рівнянь для чотирирівневої системи, нехтуючи зміною числа фотонів в типі коливань за рахунок спонтанного випромінювання.

Показати, що в наближенні, яке описується в рамках найпростіших кінетичних рівнянь, в лазері не може виникнути пульсуючий режим.

Задача 9. У пошуках ефективних систем для генерації ультракоротких імпульсів в літературі обговорювалася можливість використання для цієї мети двофотонного лазера, який працює в режимі модуляції добротності.

Оцінити час наростання лазерного імпульсу для двофотонного лазера в режимі модуляції добротності. Схема робочих рівнів наведена на (мал. 3.6). Прямий перехід заборонений. Дзеркала резонатора підібрані так, що резонатор (при включенні добротності) має різкий мінімум втрат на частоті.

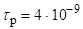
При оцінках вважати, що число часток на рівні 2 в момент включення добротності см-3 (рівень 1 порожній). Коефіцієнт Ейнштейна для двофотонного переходу с-1, час життя фотонів в резонаторі при включеній добротності с. Начальне число фотонів в момент включення добротності Nначсм-3.

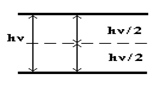
Малюнок 3.6 — До розрахунку двофотонного лазера в режимі модуляції добротності.

Задача 10. Активне середовище оптичного квантового генератора має коефіцієнт квантового посилення g і коефіцієнт втрат k. Дзеркала резонатора однакові з коефіцієнтом відображення .

Обчислити відношення когерентної вихідної потужності P0 до потужності Pk, що поглинається в активній речовині, вважаючи P0(g — k) і Pk.

Показати, що при довжині стержня активної речовини критичнішої потужності, що поглинається в зразку, стає більше потужності когерентного вихідного випромінювання і в цьому значенні оптичний квантовий генератор стає неефективним.

Задача 11. Розрахувати цезієвий лазер з оптичним накачуванням. Робочий перехід, мкм. Накачування здійснюється випромінюванням Не лампи (мкм) і призводить до перекиду атомів з основного рівня на рівень.

Відповісти на наступні чотири питання:

• 1) Яка величина максимального коефіцієнта поглинання пар цезія (лінію поглинання вважати доплерівським уширенням)?
• 2) Чи достатній цей коефіцієнт для повного поглинання сигналу накачування, якщо діаметр трубки, заповненої парами цезія при тиску тор, рівний 1 см?

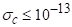
• 3) Показати, що зіткнення іншого роду не повинні грати велику роль в зміні населеності робочих рівнів. Для цього оцінити верхній кордон ймовірності передачі збудження за рахунок зіткнень іншого роду, якщо перетин такого зіткнення см -2 і показати, що ця імовірність менше ймовірностей виромінюваних переходів з робочих рівнів.
• 4) Яка різниця населеності робочих рівнів переходу?

Потужність випромінювання Не лампи, що поглинається в парах цезія, становить приблизно 0,5 мВт/см3. Вважати, що вся енергія сигналу накачування, що поглинається повністю йде на перекид атомів з рівня на рівень.

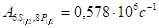
Робоча температура газу 540К, коефіцієнт Ейнштейна, відношення кратностей виродження.

.

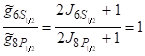
Розв`язання.

Коефіцієнт поглинання у вершині доплерівського уширення лінії рівний.

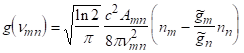
(3.31).

де — число часток в одиниці об'єму активної речовини на верхньому робочому рівні ().

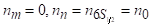
Для умов задачі верхній рівень порожній, тобто. Тоді модуль коефіцієнта поглинання.

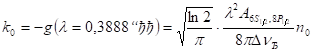
(3.32).

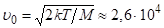
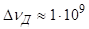
Оцінимо спочатку, де см/c, тобто Гц.

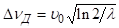
Тоді з (3.32) слідує.

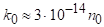
. (3.33).

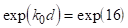
При тиску пар цезія в трубці тор і Т = 540 К см-3. Підставляючи цю цифру в (3.33), отримуємо см-1. При діаметрі газової трубки d = 1 см інтенсивність випромінювання, котре проходить крізь трубку, Не лампи послаблюється в, тобто практично повністю поглинається.

Ймовірність Рс передачі збудження за рахунок зіткнень другого роду.

(3.34).

де для атомів газу.

.

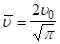
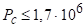
Беручи для оцінки максимальне значення, отримуємо с-1.

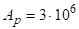
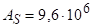
З результатів попередньої задачі маємо ймовірності переходів з рівнів і за рахунок випромінюваних переходів с -1 і с -1відповідно. Видно, що, тобто ймовірність передачі збудження за рахунок зіткнень другого роду менше ймовірності випромінюваних переходів з робочих рівнів.

Для оцінки різниці населеності будемо виходити з того, що потужність, котра затрачується на створення населеності, рівна.

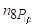
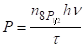
(3.35).

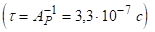
де — час спонтанного переходу з рівня .

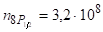
Підставляючи в (3.34) значення величин, які туди входять, в тому числі, дедовжина хвилі випромінювання Не — лампи, отримуємо см-3.

З іншого боку, з результатів попередньої задачі виходить, що частки розподіляються між рівнями і у відношенні, тобто приблизно см-3 часток переходить на рівень за рахунок спонтанних переходів. Таким чином, різниця населеності рівнів і дорівнює см-3 часток.

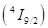
Задача 12. У багатьох випадках типовим активним середовищем лазера є, кристал (ітрій — алюмінієвий гранат,), в якому частина іонів заміщена іонами. Звичайно концентрація іонів становить 1 ат. %, тобто 1% іонів заміщений іонами. Щильність кристала рівна 4,56 г/см³. Визначити концентрацію іонів, що знаходяться на основному рівні. Насправді цей рівень складається з п’яти (двічі вирождених) рівнів, з яких чотири верхніх знаходяться на відстані від нижнього на 134, 197, 311 і 848 см-1 відповідно. Вирахувати концентрацію іонів, що знаходяться на самому нижньому рівні стану.

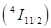
Задача 13. Верхній рівень лазера на Nd: YAG насправді складається з двох дуже пов’язаних підрівней, віддалених один від одного на (див. мал. 3. 7). Генерація відбувається на переході з підрівня верхнього рівня на підрівень нижнього лазерного рівня. Перетин даного переходу рівний. Знайдіть ефективний перетин лазерного випромінювання.

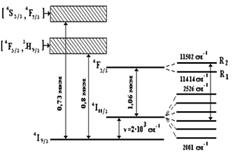
Малюнок 3.7 — Спрощена схема енергетичних рівнів кристала Nd: YAG.

Задача 14. Циліндричний стержень з Nd: YAG діаметром 6,3 мм і довжиною 7,5 см накачується могутньою імпульсною лампою. Значення перетину лазерного переходу в максимумі лінії з довжиною хвилі 1,06 мкм дорівнює, а показник заломлення рівний n = 1,82. Знайдіть критичну інверсію населеності, відповідну початку процесу посилення спонтанного випромінювання (УСИ) (передбачається, що на обидва торці лазерного стержня нанесені ідеальні просвітлюючі покриття, тобто вони не відображують світло). Крім того, обчисліть максимальну кількість енергії, яка може бути запасена в цьому стержні, якщо необхідно уникнути виникнення процесу УСИ.

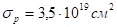
Задача 15. Лазер на Nd: YAG () діє по чотирирівневій схемі. Перетин переходу в максимумі лінії складає, а час життя мс. Обчисліть інтенсивність насичення посилення.

Задача 16. Кристалічний стержень з Nd: YAG діаметром 6,3 мм накачується лампою з внутрішнім діаметром 4 мм в еліптичному освітлювачі, велика вісь якого рівна 40 мм, а ексцентриситет рівний 0,3. Обчисліть ефективність передачі накачування, передбачивши, що середня відбивна здатність покриття освітлювача рівна 0,95 і що лампа непрозора для власного випромінювання.

Задача 17. Обчисліть час життя верхнього лазерного рівня рубінового лазера з довжиною хвилі 0,69 мкм, якщо при ефективному перетині генераційного переходу см² інтенсивність насичення становила 2 кВт/см².

Розв`язання.

Запишемо розподіл Больцмана для дворівневої системи в оптичному діапазоні.

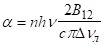
. (3.36).

Знаючи, що:

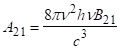
і ,.

Запишемо вираження (3.36) у вигляді.

.

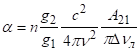
де — коефіцієнт заломлення, і - індуційні переходи, і - кратности виродження, — ширина лінії переходу, — коефіцієнт поглинання.

Перетворюємо вираження (3.37), знаючи що:

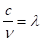
і ,.

отримуємо.

.

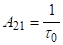
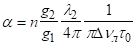
де — природний час життя частки на верхньому рівні.

Враховуючи, що отримуємо:

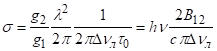
(3.37).

де — перетин поглинання.

Ефективна характеристика насичення записується.

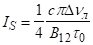
(3.38).

Підставивши у вираження (3.37) з (3.38), отримуємо.

.

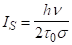
Звідки.

.

Підставимо чисельні значення.

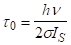
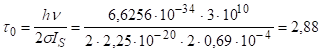
мс.

Задача 18. Обчисліть пікову потужність імпульсу рубінового лазера, працюючого в режимі модуляції добротності, якщо інверсія населеності складає см-3, довжина резонатора 15 см, довжина хвилі 0,69 мкм і втрати на відображення і розсіяння за перехід 0,06.

Розв`язання.

Пікова потужність імпульсу обчислюється по формулі.

.

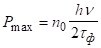
де — час життя фотона в резонаторі, — початкова інверсія.

Час життя фотона в резонаторі рівний.

.

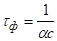
де — еквівалентний коефіцієнт поглинання.

Еквівалентний коефіцієнт поглинання рівний.

.

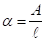
де, А — коефіцієнт поглинання енергії випромінювання за один прохід резонатора довжиною .

Підставляючи дані формули у вирази для знаходження пікової потужності імпульсу, отримуємо.

.

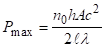
Підставимо чисельні значення:

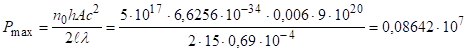
Вт/см³.

Задача 19. Довжина хвилі, що випромінюється YAG: Nd3+ - лазером, рівна мкм, поперечний перетин цього переходу см² час життя мкс. Обчислити інтенсивність насичення.

Розв`язання.

У разі насичення звичайно ми маємо справу не з об'ємною щильністю енергії, а з щильністю потоку випромінювання I, або, інакше кажучи, з інтенсивністю випромінювання енергії I. Є формула, яка дозволяє вивести деяку ефективну характеристику насичення.

.

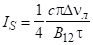
де — ширина лінії переходу,.

— коефіцієнт поглинання,.

n — щильність загального числа часток,.

— коефіцієнт Ейнштейна, для переходу з 1 рівня на 2.

Але поперечник поглинання визначається з.

.

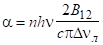
де .

Таким чином, отримуємо формулу.

;

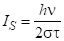
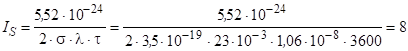
кВт/см².

Задача 20. Лазерний резонатор складається з двох дзеркал з коефіцієнтом відображення. Довжина активного середовища см, а перетин переходу см². Обчислити порогову інверсію населеності.

Розв`язання.

Зміна dF щильності потоку падаючого випромінювання, зумовлена процесами вимушеного випромінювання і процесами поглинання, в шарі dz визначається рівнянням.

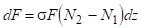
(3.39).

де — населеність рівнів, між якими відбуваються переходи при випромінюванні і поглинанні;

— перетин переходу;

F щильність потоку падаючого випромінювання.

Щоб знайти зміну щильності потоку при проходженні хвилі через все активне тіло, треба вирішити рівняння (3.39). Зробивши це, отримуємо, що посилення випромінювання за один прохід в активному середовищі дорівнює.

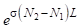
(3.40).

де L — довжина активного тіла.

Якщо втрати в резонаторі визначаються тільки пропущенням дзеркал, то поріг генерації буде досягнутий при виконанні умови.

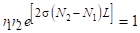
(3.41).

де — коефіцієнти відображення дзеркал.

З вираження (3.40) отримуємо формулу, що описує порогову інверсію населеності.

.

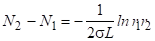
Підставляючи чисельні значення, отримуємо, що ця величина рівна см -3.

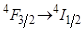
Задача 21. Квантовий вихід переходу алюмінієвого граната, а відповідний час життя нс. Обчислити спонтанний і невипромінюваний часи життя рівня .

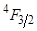
Розв`язання. Між загальним часом життя, спонтанним і невипромінюваним часами життя існує співвідношення.

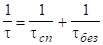
(3.42).

Крім того між квантовим виходом люмінесценції ф і часами життя і також існує співвідношення.

.

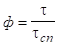
Звідки.

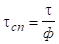
. (3.43).

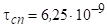
Підставляючи числові значення, отримуємо с.

Порівнюючи (3.42) і (3.43) отримуємо.

.

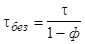
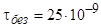
Підставляючи числові значення, отримуємо с.

Задача 22. Обчислити перетин поглинання іонів Cr3+ в рубіні з концентрацією см -3, якщо на довжині хвилі 0,54 мкм інтенсивність світла, що пройшло крізь пластину товщиною 0,5 см, падає в разі.

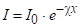
Розв`язання. Закон Бугера:. Прологарифмувавши вираження для зміни інтенсивності (закон Бугера), визначимо коефіцієнт поглинання:

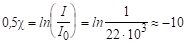
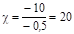
см-1.

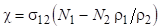
Коефіцієнт поглинання пов’язаний поперечником (перетином поглинання) співвідношенням. У стані термодинамичної рівноваги в квантовій системі N1>>N2, тому. Перетин поглинання для системи іонів, що розглядається:

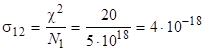
см².

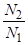
Задача 23. Відношення населеності двох рівнів, що знаходиться в термодинамичній рівновазі при Т = 300К, дорівнює. Обчислити частоту випромінювання, яка відповідає переходу між цими рівнями. Визначити, на яку область спектра електромагнітних коливань потрапляє випромінювання такої частоти (вважати).

Розв`язання.

Закон Больцмана для системи, що розглядається.

.

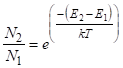
Використовуємо постулат Бору. Після логарифмування вираження.

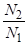
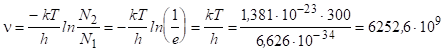
Гц.

Довжина хвилі, що випромінюється при переході.

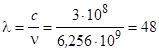
мкм.

Випромінювання падає в далекий інфрачервоний діапазон спектра.