Показові нерівності.
Нерівності

Найбільш складними являються логарифмічні нерівності, коли основи логарифмів залежать від х. Розв’яжемо нерівності методом інтервалів і находимо розв’язок. Загальний розв’язок яких утворить розв’язок нерівності (9). Логарифмічні нерівності зводяться до нерівності вигляду. Показові нерівності приводять до нерівності вигляду. Приклад. Розв’яжемо логарифмічну нерівність. Приклад. Розв’яжемо… Читати ще >
Показові нерівності. Нерівності (реферат, курсова, диплом, контрольна)
Показові нерівності приводять до нерівності вигляду.
(7).
Якщо, то .
Якщо, то .
Приклад. Розв’яжемо показові нерівності.
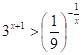
.
Перейдемо до основи 3.
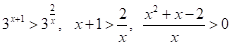
.
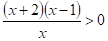
. Розв’яжемо нерівності методом інтервалів і находимо розв’язок .
Приклад. Розв’яжемо показові нерівності.
.
Запишемо нерівність у вигляді.
.
Поділимо нерівність на і отримаємо.
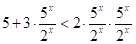
.
Позначимо, отримаємо нерівність.
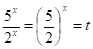
.
1) .
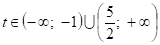
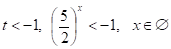
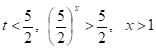
2). Відповідь .
Логарифмічні нерівності
Логарифмічні нерівності зводяться до нерівності вигляду.
(8).
- 1. Якщо, то .
- 2. Якщо, то .
Приклад. Розв’яжемо нерівність.
.
Запишемо нерівність у вигляді (8).
і знаходимо розв’язок .
Приклад. Розв’яжемо нерівність.
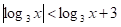
.
Запишемо нерівність у вигляді.
.
Звідси знаходимо ,.
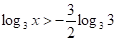
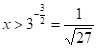
.
Найбільш складними являються логарифмічні нерівності, коли основи логарифмів залежать від х.
(9).
Приходимо до двох систем нерівностей.
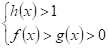
1., 2. .
Загальний розв’язок яких утворить розв’язок нерівності (9).
Приклад. Розв’яжемо нерівність.
.
Розв’яжемо систему нерівностей.
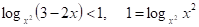
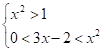
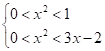
1. 2. .
Остаточна відповідь .
Приклад. Розв’яжемо логарифмічну нерівність.
.
Запишемо нерівність у вигляді (9).
і розглянемо можливі випадки.
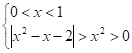
1. 2. .
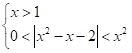
Побудуємо графік функції .
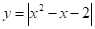
При отримаємо нерівність.
.
При отримаємо нерівність.
, .
При отримаємо нерівність.
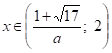
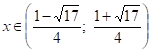
; .
Розв’язок нерівності .