Метод пошуку екстремуму в системах екстремального керування за градієнтним методом

Сутність градієнтного методу першого порядку полягає у пошуку напряму руху, що збігається з поточним напрямком вектора градієнта функції мети (при пошуку максимуму) і в протилежному йому (при пошуку мінімуму): математичний безінерційний екстремум.

.

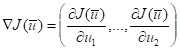
Пошук екстремуму виконується у два етапи: на першому знаходять значення частинних похідних по всім незалежним змінним, які дають напрямок градієнта в розглянутій точці.

Вони можуть бути отримані по двом вимірюванням значення у близьких точках :

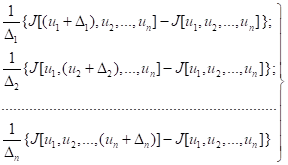
На другому пошук здійснюється у напрямку, що збігається з напрямком градієнта (для максимуму) або протилежному йому (для мінімуму) за допомогою одночасної зміни всіх незалежних змінних. Кожна з них одержує приріст, пропорційний відповідній складовій градієнта по даній осі. Алгоритм градієнтного методу може бути записаний у такий спосіб:

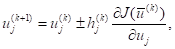
де h — робочий крок.

Тобто метод складається із двох етапів:

Виконується пробний крок для визначення величини і напряму градієнта:

де — координата вектору початкового стану, — координата вектору пробного стану, — одиничний вектор відхилення по заданій координаті, g — пробний крок.

Зміщення у напрямі градієнту по всіх осях координат:

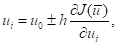
де h — робочий крок.

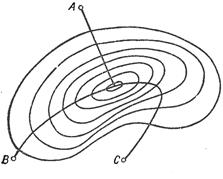
Рис. 1.

На Рис. 1 Показано траєкторії руху від початкових точок А, В, С у напрямі градієнта.

Момент закінчення пошуку екстремуму встановлюється по виконанню певних умов, подібних розглянутим. Характерна риса градієнтного методу полягає в тому, що рух при пошуку екстремуму здійснюється в загальному випадку ортогонально до поверхонь (у двомірному випадку — до ліній) постійного рівня цільової функції. Крім таких переваг, як висока точність, досить гарна збіжність, градієнтний метод першого порядку має недоліки: можливість визначення тільки локального екстремуму функції при заданих початкових умовах, порівняно великий об'єм обчислень, труднощі застосування при наявності обмеження.