Розділ 3. Розробка комплексу моделей прогнозування загрози банкрутства

Побудова моделі нечіткої нейронної мережі оцінки ризику банкрутства підприємства

Після вибору показників, які будуть служити в якості вихідних даних, і класів кризи, на які поділяється вся сукупність даних, потрібно побудувати нечітку нейронну мережу, визначальну приналежність підприємства до певного класу кризи, виходячи з початкових даних.

Для побудови нечіткої нейронної мережі була обрана програма MatLab, а саме її пакет Fuzzy Logic Toolbox, який призначений для проектування і дослідження систем на нечіткій логіці.

Навчальна вибірка складається з 36 підприємств легкої промисловості, які мають різне фінансове становище з метою віднесення їх до різних класами кризи. Вихідні класи кризи були визначені на основі Методики Міністерства Фінансів України. Були розраховані основні фінансові показники, проведений вертикальний і горизонтальний аналіз та інші процедури, описані в методиці. В результаті цього аналізу були виділені групи підприємств, які відносяться до трьох класів кризи. У першу групу входять підприємства з високим запасом фінансової стійкості, здатні виконувати свої зобов’язання і без загрози банкрутства. У другу групу входять підприємства, які відчувають деякі фінансові проблеми і мають невеликий ризик банкрутства. До третього класу кризи відносяться підприємства, фінансове становище яких перебуває у кризовому стані, їм загрожує банкрутство, вони не здатні розплачується за своїми короткостроковими і довгостроковими зобов’язаннями. Вихідні дані представлені в додатку А.

У групу з хорошим фінансовим становищем входить 14 підприємств, в групу з невеликою загрозою банкрутства — 10 підприємств, і в групу з високим ризиком банкрутства — 12 підприємств.

Початкові вибірка даних була перевірена на робастної, щоб виявити помилки в даних, так звані «викиди». В якості методу робастного оцінювання був обраний Т-критерій Грабса, як уже говорилося в пункті 2.1.

Тест для виявлення помилок, заснований на розрахунку Т-критерію Грабса, розраховується за допомогою наступної формули:

де: j = 1, 2, …, m;

— середнє арифметичне j-го ознаки;

S_j — стандартне відхилення j-го ознаки.

Розрахункове значення Т-критерію порівнюють з табличним значення за критерієм Смирнова-Грабса. Досліджуваний об'єкт є помилкою, якщо Т_р>Т_кр (Т_кр = Т_{б, n}). Розрахункове значення Т-критерію для вибірки в 36 показників при рівні значущості 0,05 дорівнює 2,99.

Всі отримані розрахункові значення за допомогою критерію Грабса не перевищують граничне значення в 2,99, тому можна зробити висновок, що у вихідних даних не було виявлено помилок або «викидів». Таким чином, вихідні дані можна використовувати для побудови моделі нечіткої нейронної мережі для оцінки ризику і запобігання банкрутству підприємства. Таблиця в якій представлені всі отримані значення для знаходиться в додатку Б.

Крім того, додатково було сформовано перевірочна вибірка з чотирьох підприємств, створена для поліпшення показників нейронної мережі та перевірки якості моделі. Додаткова вибірка представлена?? в табл. 3.1.

Після формування вибірок відбувається безпосередня побудова нечіткої нейронної мережі. Розглянемо більш детально, що із себе представляє нечітка нейронна мережа. Модель нечіткої нейронної мережі - нейронна мережа прямого поширення сигналу особливого типу. Архітектура нейронечіткої мережі ізоморфна нечіткої базі знань.

Таблиця 3.1.

Додаткова перевірочна вибірка.

У нейро-нечітких мережах використовуються диференційованих реалізації трикутних форм (множення і розподіл усіх АБО), а також гладкі функції приналежності. Це дозволяє застосовувати швидкі алгоритми навчання мережі для їх налаштування, засновані на методі зворотного поширення помилки [30, 88, 93].

Нечіткі нейронні мережі в пакеті MatLab (ANFIS) реалізовані за допомогою системи нечіткого виводу Сугено у вигляді п’ятишарової нейронної мережі прямого розповсюдження сигналу. При це призначення кожного шару є наступним:

перший шар — терми вхідних змінних;

другий шар — антецеденти (посилки) нечітких правил;

третій шар — нормалізації ступенів виконання правил;

четвертий шар — укладення правил;

п’ятий шар — агрегування результату, отриманого за різними правилами.

Дані завантажуються в MatLab і на їх основі будується первісна мережу. Нечітка нейронна мережа будується на основі методу Sub. Clustering, який попередньо розбиває вхідні змінні на кластери близьких значень. На основі субтрактивного алгоритму обчислюються центри кластерів даних. Об'єкти розглядаються як потенційні центри кластерів. Для кожного об'єкта розраховується значення так званого потенціалу, що характеризує щільність розташування інших об'єктів в його околиці. Чим густіше сусідні об'єкти розташовані до даного об'єкта, тим більше значення його потенціалу. Центром першого кластера призначають об'єкт з найбільшим потенціалом. Потім центр кластера, а також близько розташовані до нього об'єкти виключають із подальшого розгляду. Значення потенціалів залишилися об'єктів перераховують, і знову в якості центру кластера вибирають об'єкт з максимальним значенням потенціалу. Ітераційна процедура вибору центрів кластерів продовжується до тих пір, поки не будуть виключені всі об'єкти.

Вихідні параметри побудови мережі представлені на рис. 3.1.

Розглянемо початкові параметри. Range of influence — рівні впливу вхідних змінних при кластеризації. Squash factor — коефіцієнт подавлення. Значення опції використовується для визначення сусідніх до центру кластера об'єктів. Ці об'єкти вважаються належними даним кластеру і виключаються з подальшого розгляду в кластерному аналізі. Чим більше значення коефіцієнта придушення, тим більше сусідніх об'єктів будуть належати кластеру. Значення коефіцієнта подавлення дорівнює 1,25.

Accept ratio — коефіцієнт прийняття. Використовується як критерій призначення об'єкта центром кластера. Якщо відношення значень максимального потенціалу поточного центру кластера до потенціалу центру першого кластера більше коефіцієнта прийняття, тоді поточний об'єкт розглядається як центр нового кластера та кластерний аналіз продовжується. Значення коефіцієнта прийняття дорівнює 0,5.

Reject ratio — коефіцієнт відторгнення. Використовується як критерій виключення об'єкта зі списку потенційних центрів кластерів. Якщо відношення значень максимального потенціалу поточного центру кластера до потенціалу центру першого кластера менше коефіцієнта прийняття, тоді поточний об'єкт перевіряється за коефіцієнтом відторгнення. У разі, коли це відношення більше коефіцієнта відторгнення і розглянутий об'єкт розташований далеко від уже знайдених центрів кластерів, тоді він розглядається як центр нового кластера. В іншому випадку, зазначений об'єкт виключається з подальшого розгляду як потенційний центр кластера. Значення коефіцієнта відторгнення повинно бути менше значення коефіцієнта прийняття. Значення коефіцієнта відторгнення дорівнює 0,15.

Побудована нечітка нейронна мережа має структуру, представлену на рис. 3.2.

Після цього проводилося навчання мережі з метою підвищення якості побудованої моделі. На рис. 3.3 зображені параметри навчання мережі. В якості методу навчання був обраний гібридний метод, який являє собою комбінації методу найменших квадратів і методу убування зворотного градієнта. Рівень помилки навчання дорівнює 0. Також було визначено кількість циклів навчання рівне 40.

У ході навчання мережі програма ілюструє хід процесу навчання у вікні візуалізації за допомогою графіка, який зображений на рис. 3.4.

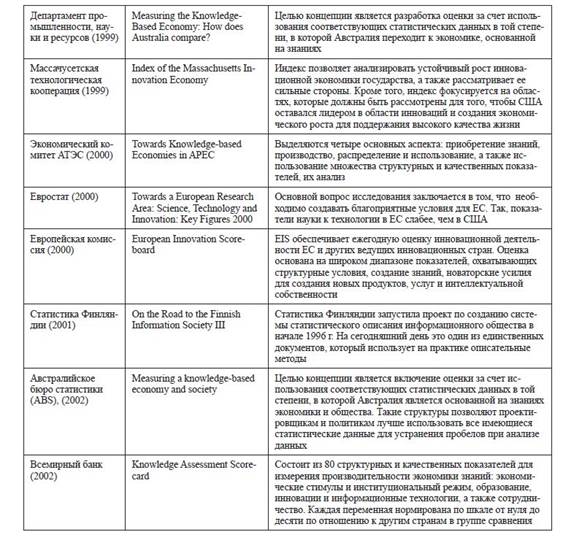
Рис. 3.4. Графік помилки навчання мережі

На графіку відбивається залежність помилки навчання від кількості циклів. Як можна помітити, помилка дуже мала і прямує до нуля.

Щоб оцінити якість побудованої нечіткої мережі, потрібно також порівняти розрахункові значення з вихідними даними. Дане порівняння проілюстровано на рис. 3.5.

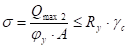
Рис. 3.5. Результат роботи нечіткої нейронної мережі

На графіку кола — це вихідні значення змінних, а зірки — це розрахункові значення, пораховані на основі побудованої мережі. Вони збігаються, що ще раз ілюструє якість побудованої мережі. Тобто побудована мережа правильно класифікує підприємства за трьома класами кризи, помилка класифікації мінімальна.

Щоб перевірити якість роботи побудованої нечіткої нейронної мережі, потрібно використовувати тестову вибірку, представлену в табл. 3.2. Завантаживши її в програму MatLab, можна побачити, як мережа обробляє нові дані і чи велика помилка. Тестова вибірка дозволяє оцінити роботу побудованої нечіткої нейронної мережі, надати їй додатковий набір даних, який дозволяє провести додаткове навчання, що підвищує її точність. На рис. 3.6 представлені результати обробки тестової вибірки.

Побудована нечітка нейронна мережа досить точно опрацювала тестову вибірку, помилка становить приблизно 7%, що є допустимою похибкою. На графіку точки — це вихідні дані, а зірки — це розрахункові значення.

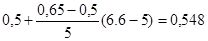
Рис. 3.6. Результати обробки тестової вибірки

На додаток до цього можна зробити візуальний аналіз правил побудованої мережі. Всього мережею було створено 13 правил для визначення приналежності, геометрична інтерпретація яких відображена на рис. 3.7.

На рис. 3.7 представлено графічне зображення функцій належності для кожного показника фінансового стану, де вертикальною лінією відзначено фактичне значення фінансового показника. В останньому стовпці можна побачити значення вихідної функції, яке в даному випадку дорівнює 1. Тобто підприємство знаходиться в доброму фінансовому стані.

Таким чином, можна сказати, що побудована нечітка нейронна мережа показала досить високу точність і хороші результати, і тепер може бути використана для діагностики загрози банкрутства підприємств легкої промисловості.