Сортування вибором. 
Порівняння загальних характеристик роботи різних методів сортування

Оцінимо часову складність даного методу, використовуючи в якості основної операції операцію порівняння.

Для пошуку мінімального елемента в кожному проході потрібно виконати: n-1, n-2, 1 операцій порівняння, тобто всього n (n-1) / 2 операцій порівняння. Отже, обчислювальна складність даного методу O (n2). Причому час сортування не залежить від вихідного порядку елементів.

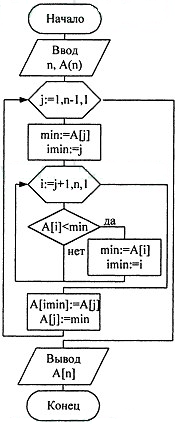
Рисунок 3.1 — Алгоритм сортування вибором.

Метод швидкого сортування

Загальний аналіз ефективності «швидкої» сортування досить важкий. Буде краще показати її обчислювальну складність, підрахувавши число порівнянь при деяких ідеальних припущеннях. Припустимо, що n — ступінь двійки, n = 2k (k = log2n), а центральний елемент розташовується точно посередині кожного списку і розбиває його на два підсписки приблизно однакової довжини.

При першому скануванні проводиться n-1 порівнянь. В результаті створюються два підсписки розміром n / 2. На наступній фазі обробка кожного підсписки вимагає приблизно n / 2 порівнянь. Загальне число порівнянь на цій фазі дорівнює 2 (n / 2) = n. На наступній фазі обробляються чотири підсписки, що вимагає 4 (n / 4) порівнянь, і т.д. Зрештою процес розбиття припиняється після k проходів, коли вийшли підсписки містять по одному елементу. Загальне число порівнянь приблизно дорівнює n + 2 (n / 2) + 4 (n / 4) + … + N (n / n) = n + n + … + N = n * k = n * log2n.

Для списку загального вигляду обчислювальна складність «швидкої» сортування дорівнює O (n log2 n). Ідеальний випадок, який ми тільки що розглянули, фактично виникає тоді, коли масив вже відсортований за зростанням. Тоді центральний елемент потрапляє точно в середину кожного підсписки.

Якщо масив відсортований за спаданням, то на першому проході центральний елемент виявляється на середині списку і змінюється місцями з кожним елементом як у першому, так і в другому підсписки. Результуючий список майже відсортований, алгоритм має складність порядку O (n log2n).(рис. 3.2.1).

Найгіршим сценарієм для «швидкої» сортування буде той, при якому центральний елемент весь час потрапляє в одноелементні подспісок, а всі інші елементи залишаються в другому підсписки. Це відбувається тоді, коли центральним завжди є найменший елемент. Розглянемо послідовність 3, 8, 1, 5, 9.

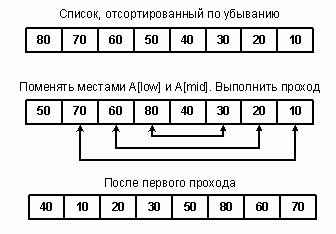
Рисунок 3.2.1?опис методу швидкого сортування На першому проході проводиться n порівнянь, а більший подспісок містить n-1 елементів. На наступному проході цей подспісок вимагає n-1 порівнянь і дає подспісок з n-2 елементів і т.д. Загальне число порівнянь одно: n + n-1 + n-2 + … + 2 = n (n +1) / 2 — 1.

Складність найгіршого випадку дорівнює O (n2), тобто не краще, ніж для сортувань вставками і вибором. Однак цей випадок є патологічним і малоймовірний на практиці. Загалом, середня продуктивність «швидкої» сортування вище, ніж у всіх розглянутих нами сортувань.

Алгоритм QuickSort вибирається за основу в більшості універсальних сортують утиліт. Якщо ви не можете змиритися з продуктивністю найгіршого випадку, використовуйте пірамідальну сортування — більш стійкий алгоритм, складність якого дорівнює O (n log2n) і залежить тільки від розміру списку.

3.4 Метод сортування бульбашкою

Алгоритм метод бульбашки — найбільш простий метод сортування масиву. Через своєї простоти цей метод не дуже ефективний і вимагає процесорного часу більше, ніж інші методи. Однак для сортування невеликих масивів використання методу бульбашки прийнятно. Припустимо, що масив сортується в порядку зростання, тоді метод бульбашки використовує цикл за значеннями масиву, переміщаючи поступово найбільше значення в кінець масиву (подібно до того, як в воді спливає на поверхню пляшечку).

Сортування методом бульбашки займає 61,3 секунд.