Функціональні рівняння і групи

Де нові невідомі не виникли — побудована система чотирьох лінійних рівнянь (3) — (6) з чотирма невідомими, і. Послідовно виключаючи, знайдемо. Як і при розв’язанні рівняння (1), ми припускали, що функція, яка задовольняє (3), існує. Перевірка показує, що f задовольняє рівнянню (3). Розв’язання. Припустимо, що існує функція f (x), що задовольняє даному рівнянню. Замінивши х на 1-х, одержимо. Разом… Читати ще >
Функціональні рівняння і групи (реферат, курсова, диплом, контрольна)
Композиція функцій
Число початкових, основних функцій, що вивчаються в шкільному курсі математики, порівняно невелике. До них, наприклад, відносяться лінійна, сттепенева, показникова, тригонометрична функції. Інші функції виходять з основних за допомогою композицій і дій алгебри. Так, функція f (x) sin (2x + 1) є композицією лінійної функції g (x)2x+1 і тригонометричної функції h (x)sin x тобто f (x)h (g (x)) (h?g)(x). Функція f (x)lg arcsin x одержана в результаті композиції функцій.
g (x)arcsin х і h (x)lg x.
Зверніть увагу на те, що в область визначення композиції h? g входять i значення х з D (g), для яких g (x) D (h). У останньому прикладі D (g)=[-1;1], D (h)=(0;). Оскільки arcsin х>0 при х (0;1), то D (f)=(0;1).
Якщо узяти композицію цих же функцій в зворотному порядку, тобто функцію f (x)=arcsin lg х, то одержимо:
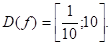
Композицією дробово-лінійних функцій і є функція.
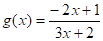
Тут.
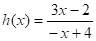
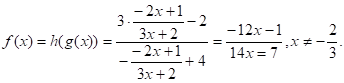
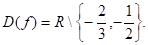
Як правило, f? g g? f. В той же час для будь-яких функцій (f?g)?h = f?(g?h),.
що безпосередньо витікає з визначення композиції.
Функціональні рівняння
Розв’яжимо наступну задачу.
Задача 1. Знайдіть всі функції y=f (x) такі, що.
2f (1-х)+1= xf (x). (1).
Розв’язання. Припустимо, що існує функція f (x), що задовольняє даному рівнянню. Замінивши х на 1-х, одержимо.
2f (х)+1= (1-х)f (1-х). (2).
З (1) знаходимо f (1-х)= (xf (x)-1).
Підставляючи значення f (1-х) і рівняння (2), одержимо.
2f (х)+1= (1-х)· (xf (x)-1), звідки.
Безпосередньою перевіркою переконуємося, що одержана функція задовольняє рівнянню (1).
У розглянутому рівнянні під знаком невідомої функції стоять функції і. Заміна х на 1-х переводить функції і один в одного. В результаті підстановки х 1-х одержано ще одне рівняння, що містить f (x) і f (1 -х). Рішення функціонального рівняння ми звели до розв’язання системи двох лінійних рівнянь з двома невідомими.
Розглянемо тепер складнішу задачу.
Задача 2. Вирішіть рівняння.
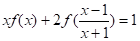
. (3).
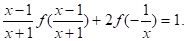
Рішення. Спробуємо діяти так само, як і в першому випадку. Виконаємо заміну. Одержуємо (4).
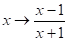
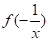
Разом з виразами і у нас з’явилося нове «невідоме» — Спробуємо застосувати в (3) ще одну підстановку:
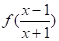
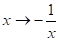
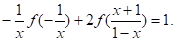
Маємо (5).
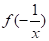
Окрім, в рівнянні з’явився «небажаний» вираз.
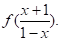
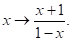
Що ж, спробуємо виконати в (3) підстановку І, нарешті, успіх. Одержуємо рівняння (6).
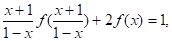
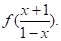
де нові невідомі не виникли — побудована система чотирьох лінійних рівнянь (3) — (6) з чотирма невідомими, і. Послідовно виключаючи, знайдемо.
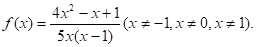
Як і при розв’язанні рівняння (1), ми припускали, що функція, яка задовольняє (3), існує. Перевірка показує, що f задовольняє рівнянню (3).