Ієрархічний кластерний аналіз

Кластерний аналіз — це сукупність методу, що дозволяють класифікувати багатомірність спостереження за відсутності апріорної інформації про розподіл генеральної сукупності з якої зроблено вибірку досліджуваних об'єктів.

Мета кластерного аналізу — утворення груп, схожих між собою об'єктів, які називаються кластерами.

Кластерний аналіз призводить до розбиття на групи з урахуванням всіх ознак одночасно. В кластерному аналізі використовується принцип утворення груп — політетичний підхід, немає чітко визначених меж груп.

Кластерний аналіз важливе місце займає в тих галузях науки, які пов’язані з вивченням масових явищ і процесах. Його методи допомагають виявити внутрішні зв’язки між одиницями спостережуваної сукупності, можуть використовуватися з метою стиснення інформації.

Методи кластерного аналізу вирішують наступні задачі:

• 1. Розбиття вхідних сукупних ознак на порівняно невелику кількість кластерів, так щоб елементи першого кластера були максимально подібними між собою.
• 2. Визначення природного чіткого розшарування всіх об'єктів на чітко вираженні кластери, які розташовані на значній відстані один від одного.

Методи кластерного аналізу:

• — агломеративні;
• — дивизимні;
• — ітераційні.

Використаємо як спосіб вимірювання евклідову відстань:

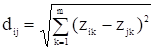
(2.6).

Оцінка розбиття на кластери проводиться за допомогою функціоналу якості розбиття. Використовуються наступні види функціоналів:

1) загальна сума внутрішньо — групових дисперсій:

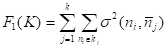
(2.7).

2) загальна сума попарних внутрішньо — кластерних відстаней між елементами:

3) узагальнена внутрішньо — класова дисперсія:

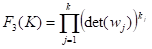
(2.9).

У формулах: — кількість кластерів;

— вектор середніх значень ознак об'єктівго кластера;

— дисперсія об'єктівго кластера;

— коваріаційна матриця об'єктівго кластера;

— кількість об'єктів, що належатьму кластеру.

Найчастіше використовують перший та другий функціонал. Найкращим вважається таке розбиття при якому функціонал досягає свого екстремального (min) значення.