Розвиток теорії меж

Понятие предела и понятие функции — фундаментальные понятия математического анализа. Начало изучению понятия предела положено в элементарной математике, где с помощью предельных переходов определяются длина окружности, объём цилиндра, конуса и т. д. Оно также было использовано при определении суммы бесконечно убывающей геометрической прогрессии. Операция предельного перехода является одной из основных операций анализа.

Предемл фумнкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится значение рассматриваемой функции при стремлении её аргумента к данной точке.

Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.

Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).

В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т. н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.

Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».

Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений существует окрестность этого значения такая, что в любой сколь угодно малой окрестности точки, в которой функция принимает заданное значение, существуют точки, значение функции в которых окажется за пределами указанной окрестности.

Если в некоторой точке области определения функции существует предел и этот предел равен значению функции в данной точке, то функция оказывается непрерывной (в данной точке).

Пусть функция определена в некоторой окрестности точки а, кроме, может быть, самой точки а.

Число В называется пределом функции в точке, а (или при ), если для любой последовательности значений аргумента , последовательность соответствующих значений функции, сходится к числу В

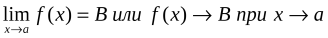
Число, А называется пределом функции в точке x=х0 (или при), если для любой сходящейся к х0последовательности (1) значении аргумента x, отличных от х0, соответствующая последовательность (2) значений функции сходится к числу А. Обозначается .

Функция может иметь в точке х0 только один предел. Это следует из того, что последовательность имеет только один предел.

Примеры.

1). Функция =с=const имеет предел в каждой точке х0 числовой прямой, т. е.

gif" name="object9″ align=absmiddle width=63 height=29>

2). Функция =x имеет в любой точке х0 числовой прямой предел, равныйх0, т. е.

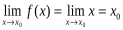
Определение 2. Число А называется пределом функции в точке х=х0, если для любого числа существует число такое, что для всех, удовлетворяющих неравенству, выполняется неравенство. предельный функция числовой множитель Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением ''на языке последовательностей'', или определением по Гейне (1821−1881 — немецкий математик). Второе определение называют определение на языке '', или определением по Коши (1789−1857 — французский математик).

Можно доказать, что оба определения предела функции в точке х0эквивалентны, а это значит, что можно использовать любое из них в зависимости от того какое более удобно при решении той или иной задачи.

Кроме рассмотренного понятия предела функции при существует также понятие предела функции при .

Определение. Число А называется пределом функции при, если для любого Е>0 можно указать такое положительное число N, что для всех значений x, удовлетворяющих неравенству, будет выполнятся неравенство .

Основные свойства пределов функций:

1. Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют:

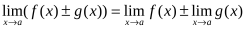
2. Предел произведения функций равен произведению их пределов, если последние существуют:

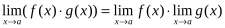
Следствие. Постоянный множитель можно выносить за знак предела:, если предел существует.

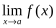
3. Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля:

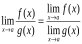
если .

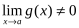
Пример. Вычислить пределы:1., 2., 3.

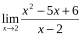
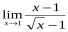
Решение.1. ;

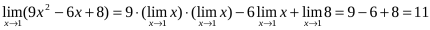
2. Поскольку предел знаменателя равен 0, то воспользоваться теоремой о пределе частного невозможно. Поэтому первоначально сократим дробь, разложив числитель и знаменатель на множители:

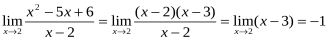
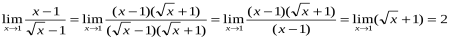
Заключение

В развитии теории пределов принимали участие И. Ньютон, Г. Лейбниц, Ж. Даламбер, Л.Эйлер. Современная теория предела основана на строгом определении предела, данном О. Коши, и была существенно продвинута работами математиков 19 века К. Вейерштрасса и Б.Больцано.