Зв'язок з трекутником Паскаля

Між числами Фібоначчі і трикутником Паскаля існує цікавий зв’язок. Проведемо через трикутник лінії, під кутом 45 градусів до його рядків, як показано на мал.1 і назвемо їх висхідними діагоналями. Розрахуємо для кожної висхідної діагоналі суму всіх чисел, що стоять в цій діагоналі. Отримаємо для першої діагоналі 1, для другої 1, для третьої 2, для четвертої 3, для п’ятої 5, для шостої 8, для сьомої 13. Ми отримали перші сім чисел Фібоначчі. Виявляється, що завжди сума чисел n-ї діагоналі є n-е число Фібоначчі. Дійсно, для n = 1 і n = 2 збіг видно безпосередньо, для наступних значень n збіг пояснюється тим, що суми вирахувані для будь-яких двох послідовних діагоналей будучі складені один з одним дають суму вирахувану для слідкуючої за ними діагоналі. З рівності (1) ми маємо, що сума всіх членів трикутника Паскаля, що лежать на самій n-й діагоналі так і вище її рівна un+2 — 1.

Числа Фібоначчі як деяка функція їх номерів

До цього часу ми визначали число Фібоначчі по його номеру. Проте, будь-яке число Фібоначчі можна подати у вигляді деякої функції його номера. Послідовність Фібоначчі є рекурентне співвідношення другого порядку з постійними коефіцієнтами. Оскільки, рекурентні співвідношення не є предметом дослідження даної роботи, алгоритм їх розв’язання буде наведений без доведень:

Нехай дано рекурентне співвідношення:

u n+2 = a 1 u n +1 + a 2 u n. (9).

Складемо квадратне рівняння:

r2 = a 1 r + a 2 (10).

яке називається характеристичним для даного співвідношення, якщо рівняння (10) має два різні корені r1 і r2 то спільне рішення рекурентного співвідношення має вигляд:

f (n) = C1 r1n-1 + C2 r2n-2 (11).

При вивченні послідовності Фібоначчі, ми прийшли до рекурентного співвідношення:

u n = a 1 u n -1 + a 2 u n-2.

Для нього характеристичне рівняння має вигляд:

r2 = r + 1.

Коренями цього квадратного рівняння є числа:

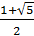
r1 =, r2 = .

Тому спільне рішення співвідношення Фібоначчі має вигляд:

f (n) = C1 ()n + C2 ()n. (12).

Так як будь-яке рішення рекурентного співвідношення другого порядку визначається u1 і u 2, тому з рівнянь:

С1 + С2 = u1,.

С1 r1 + С2 r2 = u2,.

тобто:

С1 + С2 =1.

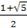
С1 () + С2 () = 1.

Розв’язавши цю систему, ми отримаємо:

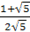
C1 =, C2 = ;

З рівняння (12):

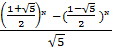
un = (13).

Формула (13) називається формулою Бине (по імені математика, який його вивів).