Лінійне тригонометричне рівняння

Тригонометричне рівняння перетворюють до виду де — тригонометричний вираз, наприклад. Або звідки дістаємо розв’язок Умова, за якої рівняння (1) можна розв’язати, така: Якщо ліву частину рівняння вдається подати у вигляді добутку двох множників: Рівняння тригонометричне лінійне система Рівняння має такий розв’язок: Називається однорідним. Якщо розподілимо обидві частини рівняння на. Називається… Читати ще >
Лінійне тригонометричне рівняння (реферат, курсова, диплом, контрольна)
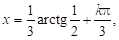
Тригонометричне рівняння.
(1).
називається лінійним. Воно зводиться до найпростіших рівнянь.
Поділимо обидві частини рівняння на вираз.
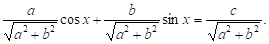
Уведемо допоміжний кут такий що.
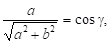
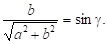
Рівняння набирає вигляду:
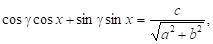
Або звідки дістаємо розв’язок Умова, за якої рівняння (1) можна розв’язати, така:
(2).
Приклад. Розв’язати рівняння.
Поділимо обидві частини рівняння на.
Або Остаточно маємо:
Зведення тригонометричного рівняння до алгебраїчного
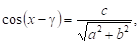



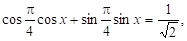
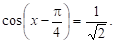

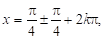
Тригонометричне рівняння перетворюють до виду де — тригонометричний вираз, наприклад.
Приклад. Розв’язати рівняння.
Усі члени рівняння подамо через функцію.
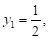
рівняння тригонометричне лінійне система Рівняння має такий розв’язок:

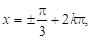
Рівняння виду.
(31).
називається однорідним. Якщо розподілимо обидві частини рівняння на.
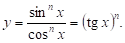
Приклад. Розв’язати тригонометричне рівняння.
Запишемо рівняння у вигляді.
Або Це рівняння однорідне, і його можна подати у вигляді:
Маємо два розв’язки:
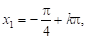
Наведемо в загальному вигляді типові заміни:
Розклад рівняння на множники
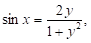
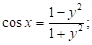
Якщо ліву частину рівняння вдається подати у вигляді добутку двох множників:

то можна окремо розв’язувати кожне з рівнянь.
і.
Приклад. Розв’язати рівняння.
Розкладемо рівняння на множники:
Оскільки то рівняння набирає вигляду.
і зводиться до двох рівнянь:

Рівняння має ті самі розв’язки, що й рівняння.