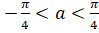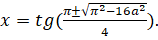Тригонометричні рівняння з параметрами

Тригонометричне рівняння з параметром — це такий тип рівнянь, коли невідома величина знаходиться під знаком тригонометричних функцій, а в лівій, або правій, або в обох частинах якого є параметр, або параметри.

Найпростішими тригонометричними рівняннями називаються рівняння sinx = a; cosx = a; tgx = a; ctgx = a. Розв’язати найпростіше тригонометричне рівняння — означає знайти множину всіх кутів, що мають дане значення a тригонометричної функції. Якщо рівняння не э найпростішим, то його треба звести до найпростішого.

Для успішного вирішення тригонометричного рівняння з параметром, слід пам’ятати наступне:

• 1) Всі тригонометричні формули (основні тригонометричні формули, формули подвійних кутів, формули зниження степеню, формули перетворення добуту в суму, формули перетворення суми в добуток, універсальні тригонометричні підстановки тощо);
• 2) Періоди тригонометричних функцій (у функцій sin x, cos x період 2П, у tg x, ctg x період П;
• 3) Обмеженість функцій (cos x, sin x за модулем одиницею);
• 4) Формули зведення;
• 5) Метод заміни змінної;
• 6) Метод введення допоміжного кута;
• 7) Метод вирішення однорідних тригонометричних рівнянь (поділити обидві частини рівняння на старших аргумент, який не дорівнює нулю).

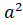
Приклад 1. Розв’язати рівняння (arctgx)(arcctgx) = .

Розв’язання:

Маємо рівняння з аркфункціями. Але рівняння має параметр а, тому визначаємо, що треба розглянути два можливих значення параметра:

а = 0 і а? 0. Коли а = 0, то (arctgx)(arcctgx) = 0, ?arctgx = 0,? x = 0.

Тут врахована властивість оберненої функції 0 < arcctgx <�р, тобто.

arcctg x? 0, враховуючи, що arctgx + arcctgx = р/2.

Звідки arcctgx = р/2 — arctgx, після підстановки отримуємо квадратне рівняння відносно arctgx = y:

.

.

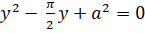
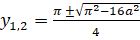
Отже, значення y дійсні, коли.

.

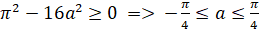
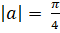
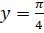
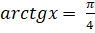
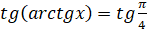
Коли, то і. Звідси, => x=1.

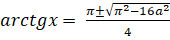
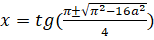
Коли, маємо => .

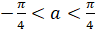
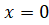
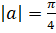
Відповідь: Якщо a=0, то; коли, x=1; при,.