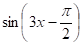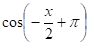Періодичні функції. 
Функції і їх графіки

Дуже багато процесів і явищ, з якими ми зустрічаємося на практиці, мають повторюваний характер. Так, взаємне розташування Сонця і Землі повторюється через рік. Положення маятника в моменти часу, що відрізняються на період коливання маятника, однакові.

Такого роду процеси називають періодичними, а функції, їхній що описують, — періодичними функціями.

Відомі вам основні тригонометричні функції — періодичні. Так для будь-якого числа x і будь-якого цілого k виконана рівність. Звідси випливає, що — період функції синус (— довільне ціле число).

Узагалі, говорячи про періодичність функції f, думають, що мається таке число, що область визначення разом з кожною точкою x містить і точки, що виходять з x рівнобіжними переносами уздовж осі Ox (вправо і вліво) на відстань T. Функцію f називають періодичної з періодом, якщо для будь-якого x з області визначення значення цієї функції в точках x, x — T і x + T рівні, тобто .

Оскільки синус і косинус визначені на всій числовій прямій і, для кожного, синус і косинус — періодичні функції з періодом .

Тангенс і котангенс — періодичні функції з періодом. Справді, області визначення цих функцій разом з кожним містять числа й і вірні рівності, .

Очевидно, що якщо функція f періодична з періодом T, те при будь-якім цілому число теж період цієї функції. Наприклад, при, скориставшись кілька разів визначенням періодичної функції, знаходимо:

Запам"ятаємо, що:

• а) найменший додатний період функцій і дорівнює ;
• б) найменшим додатним періодом функцій і є число .

Періодичністю основних тригонометричних функцій ми уже фактично користалися раніше, при побудові графіків. Справедливо наступне твердження:

Для побудови графіка періодичної функції з періодом досить провести побудова на відрізку довжиною і потім отриманий графік паралельно перенести на відстані вправо і вліво уздовж осі (рис. 34, тут — будь-яке натуральне число).

Рис. 14.20

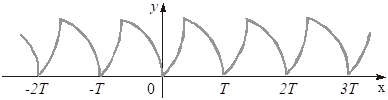
Приклад 5. Побудуємо графік функції .

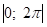
Для побудови скористаємося тим, що функція періодична з періодом. Дійсно, функція визначена на всієї прямої, і, виходить, разом з довільною точкою її область визначення містить точки, що виходять з рівнобіжними переносами уздовж осі вправо і вліво на. Крім того, унаслідок періодичності косинуса. Користаючись властивістю графіків періодичних функцій, будуємо графік спочатку на відрізку (для цього відповідно до відомих правил перетворення графіків розтягуємо графік косинуса уздовж осі в 2 рази і зрушуємо його на 1 нагору (рис. 14.21), а потім за допомогою паралельних переносів продовжуємо його на всю числову пряму (рис. 14.22).

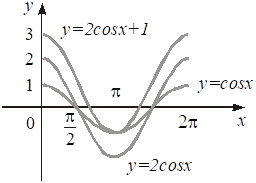
Рис. 14.21.

Рис. 14.22.

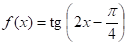
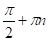
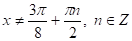
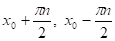
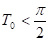
Приклад 6. Доведемо, що функція періодична і її найменший додатний період дорівнює. Тангенс визначений при всіх значеннях аргументу, не рівних,. Тому область визначення даної функції складається з таких, що, тобто. Звідси випливає, що поряд з довільним містить і всі точки виду,. Очевидно, що число є періодом, тому що. Залишається довести, що число — найменший додатний період. Допустимо, що періодом є таке число, що. Тоді для будь-якого справедливо рівність.

.

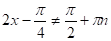
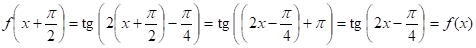
оскільки — період. Але це означає, що — період функції. По припущенню, тобто. Протиріччя з доведеним раніше: найменший додатний період тангенса дорівнює .

Аналогічно доводиться загальне твердження:

Якщо функція періодична і має період, то функція, де і постійні, а, також періодична, причому її період дорівнює .

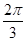
З того твердження відразу одержуємо, що, наприклад, періодом функції є число, а період функції дорівнює .