Система вправ для усних обчислень

Вправи з усних обчислень мають пронизувати увесь урок. Їх можна поєднувати з перевіркою домашніх завдань, закріпленням вивченого матеріалу, опитуванням учнів. Поряд з цим у практиці роботи вчителів є хороша традиція: на кожному уроці спеціально відводити 5−7 хв для усних обчислень, проводити так звану усну лічбу. Матеріал для цього етапу уроку вчитель запозичує з підручника, а також із спеціальних збірників усних задач і вправ.

Щоб навички усних обчислень постійно вдосконалювались, треба встановити правильне співвідношення в застосуванні усних і письмових прийомів обчислень, а саме обчислювати письмово тільки тоді, коли усно обчислити важко [13, 56].

Прийоми як усних, так і письмових обчислень ґрунтуються на знанні нумерації, конкретного змісту і властивостей арифметичних дій, зв’язку між результатами та компонентами дій, а також на знанні зміни результатів дій залежно від зміни одного з компонентів. Проте між прийомами усних і письмових обчислень є істотні відмінності:

1) Усні обчислення виконують, починаючи з одиниць вищого розряду, а письмові - з нижчого (винятком є ділення). Наприклад:

Обчислення виконано усно: його виконують, починаючи з одиниць вищого розряду.

450 + 120 = (400 + 50) + (100 + 20) = (400 + 100) + (50 + 20) =.

= 500 + 70 = 570.

Обчислення виконано письмово: його виконують, починаючи одиниць нижчого розряду.

357+246=603.

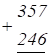
• 2) Проміжні результати під час усних обчислень зберігають у пам’яті, під час письмових — відразу записують.
• 3) Прийоми усних обчислень для тієї самої дії над парою чисел можуть бути різні залежно від особливостей прикладу і тієї властивості, яку використовують, а письмові обчислення виконують за точніше окресленим правилом, прийнятим для кожної арифметичної дій.

Наприклад:

• 1) 48· 15=48·(10+5)= 48· 10+48·5=480+240=720
• 48· 15=48·(5·3)=48·5·3=240·3=720
• 48· 15=(40+8)·15=40·15+8·15=600+120=720
• 2) 31· 24=186

Використовуються різні прийоми усних обчислень і завжди той самий прийом письмового множення.

• 4) Розв’язування під час усних обчислень записують у рядок (якщо це потрібно), а в письмових обчисленнях — стовпчиком.
• 5) Усні обчислення звичайно виконують над числами в межах 100 і над багатоцифровими числами, якщо обчислення над ними зводяться до випадків у межах 100, а письмово виконують дії над багатоцифровими числами тоді, коли усно обчислити важко.

Обчислювальні терміни вивчають у тісному зв’язку з розглядом певних питань теорії. Питання про місце введення обчислювальних прийомів та методику їх вивчення розглянуто у відповідних концентрах.

Виховуючи любов до усних вправ, вчитель допомагає учням активно працювати з навчальним матеріалом, пробуджує у них прагнення удосконалювати способи обчислень і розв’язування задач, менш раціональні замінювати досконалішими та економнішими. А це — важлива умова свідомого засвоєння матеріалу. Спрямованість мислительної діяльності на пошук раціональних шляхів розв’язання проблеми свідчить про варіативність мислення [11, 57].

Розв’язуючи певну задачу, обчислюючи вираз, учень повинен уважно розглянути умову завдання, зуміти помітити всі його особливості і в кожному конкретному випадку обрати ті шляхи, які простіше й швидше приводять до мети. Таким чином, при виконанні усних обчислень можна говорити про критичність мислення, тобто уміння оцінити запропоновані варіанти розв’язання і обрати більш раціональний підхід до виконання даного завдання.

Усні вправи також сприяють розвитку мовлення учнів, якщо з самого початку навчання вводити в тексти завдань і використовувати при обговоренні вправ математичні терміни. Навички правильного, точного і лаконічного мовлення, що формуються на уроках математики, позитивно впливають на загальну мовленнєву культуру. Важливо, щоб вчитель сам слідкував за своїм мовленням і формулював завдання ясно, чітко, лаконічно і послідовно.

Навички усних обчислень формують у процесі виконання учнями різних вправ. Розглянемо основні види їх.

1. Знаходження значень математичних виразів. Для вправ пропонують у тій або іншій формі математичний вираз, треба знайти його значення. Ці вправи мають багато варіантів. Можна пропонувати числові математичні вирази і буквені (вираз із змінною), при цьому буквам надають числових значень і визначають числове значення знайденого виразу.

Наприклад:

Знайдіть різницю чисел 100 і 9.

Знайдіть значення виразу с-k, якщо с=100, k=9.

Вирази можна запропонувати в різній словесній формі: від 100 відняти 9; 100 мінус 9; зменшуване 100, від'ємник 9, знайти різницю; знайти різницю чисел 100 і 9; зменшити 100 на 9 і т.д. Ці формулювання використовує не тільки вчитель, а й учні.

Вирази можуть бути на одну і більш як на одну дію. Вирази з кількома діями можуть містити дії одного ступеня або різних ступенів, наприклад: 47+24−56, 72:12· 9, 400−70· 4 тощо; можуть бути з дужками або без дужок: (90−42):3, 90 — 42:3.

Як і вирази на одну дію, вирази на кілька дій мають різне словесне формулювання, наприклад: від 90 відняти частку чисел 42 і 3; зменшуване 90, а від'ємник виражений часткою чисел 42 і 3 та ін.

Вирази можуть бути задані в різній області чисел: з одноцифровими числами (7−4), з двоцифровими (70−40, 72−48), з трицифровими (700−400, 720−480) і т.д., з абстрактними та іменованими числами (200−15, 2 м-15 см). Однак, як правило, прийоми усних обчислень повинні зводитися до дій над числами в межах 100. Так випадок віднімання чотирицифрових чисел 7200 — 4800 зводиться до віднімання двоцифрових чисел (72 сот. — 48 сот.), отже, його можна давати для усних обчислень.

Вираз можна дати у формі прикладу (усно або у вигляді запису): 7+2, 30−24:6. А можна дати і в інших формах, наприклад у формі таблиці:

У 1 класі для цієї мети можна використати цікаві фігури.

Завдання на знаходження значень виразів можна безпосередньо пов’язувати з різними питаннями початкового курсу математики: з нумерацією, величинами, дробами тощо. Наприклад, знайти різницю найменшого трицифрового числа і найбільшого одноцифрового; знайти, скільки сантиметрів в 1/5 м тощо.

Основне призначення вправ на знаходження значень виразів — виробити в учнів міцні обчислювальні навички. Водночас вправи на знаходження значень виразів сприяють і засвоєнню питань теорії арифметичних дій.

• 2. Порівняння математичних виразів. Ці вправи мають варіанти. Можна взяти два вирази і встановити, чи рівні їхні значення, а якщо не рівні, то яке з них більше чи менше. Наприклад, треба порівняти вирази і замість зірочок поставити знак,>",<�" або,=":
• 6 + 4 * 4 + 6 20 + 7 * 20 + 5
• 20 · 8 * 1 8 · 10 8 · 9 + 8 * 8 · 10

При цьому знак відношення можна вибрати на основі або знаходження значень даних виразів і порівняння їх (20· 8<18·10, оскільки 160 20 + 5) тощо.

Можна запропонувати вправи, які вже мають знак відношення і один із виразів, а другий вираз треба скласти або доповнити. Наприклад, треба закінчити запис: 8 · (10 + 2) = 8 · 10 + …

Можна пропонувати вправи на порівняння виразів із змінною, наприклад, замість зірочки треба поставити знак «>», «<�» або «=», наприклад: а-17 * а •12.

Вирази в таких вправах можуть включати різний числовий матеріал: одноцифрові, двоцифрові, трицифрові числа і т.д.; абстрактні та іменовані числа. Вирази можуть бути з різними діями. Основне завдання таких вправ — сприяти засвоєнню теоретичних знань про арифметичні дії, їх властивості, рівності, нерівності тощо. Крім того, вправи на порівняння виразів допомагають і виробленню обчислювальних навичок.

3. Розв’язування рівнянь. Як усні вправи пропонують рівняння. Це насамперед найпростіші рівняння (х+2=10) і складніші (15· х- 9 = 51).

Рівняння можна пропонувати в різних формах, наприклад:

Розв’яжіть рівняння 24: х = 3.

Від якого числа треба відняти 18, щоб дістати 40?

Знайдіть невідоме число: 73-х = 73 — 18.

Я задумала число, помножила його на 5 і дістала 85. Яке число я задумала?

Призначення таких вправ — виробити вміння розв’язувати рівняння, допомогти учням засвоїти зв’язки між компонентами і результатами арифметичних дій, а також сприяти виробленню обчислювальних навичок.

4. Розв’язування задач. Для усної роботи пропонують як прості, так і складені задачі. Мета цих вправ — виробити в учнів уміння розв’язувати задачі, допомогти засвоєнню теоретичних знань і виробленню обчислювальних навичок.

Під час роботи в школі учителі змінюють і доповнюють основні види усних вправ. Різноманітність вправ збуджує інтерес у дітей, активізує їхню розумову діяльність [11, 57].

У початкових класах методисти рекомендують якомога більше усних вправ проводити у формі гри. Розглянемо найпоширеніші математичні ігри.

Гра, Мовчанка". Для гри беруть яку-небудь геометричну фігуру, у центрі якої і по контуру записують числа. Біля числа, розміщеного в центрі, ставлять знак однієї з арифметичних дій. Сталим є число, записане в центрі. Гру проводять так: учитель показує указкою на одне з чисел, записаних по контуру, а діти виконують зазначену дію цього числа з числом, записаним у центрі. Викликаний учень записує результат. Решта учнів підняттям руки сигналізує про допущену помилку. Всю роботу виконують мовчки. Гру можна змінити: учитель показує на число, а діти мовчки показують результат на розрізних цифрах. Великий інтерес викликають у дітей красиво оформлені «мовчанки», наприклад, Хто найкращий капітан чи космонавт?".

Колові приклади.

• 32: 4 36 — 9 24: 8
• 3 · 12 8 + 16 27 + 5

Це колові приклади. Їх складають так: перший приклад беруть довільно (32:4), результат цього прикладу повинен бути першим компонентом наступного прикладу (8+16), результат цього прикладу буде першим компонентом прикладу (24:8) і т.д., результат останнього прикладу буде першим компонентом першого (32). Потім ці приклади записують у довільному порядку.

Гру проводять так: приклади записують на дошці або на плакаті; учні розв’язують перший приклад; викликаний учень називає не результат, а той приклад, який починається з числа, що дорівнює результату (8+16); діти розв’язують цей приклад і називають наступний, що починається з результату останнього прикладу: 24:8 і т. ін., поки не дістануть першого прикладу [9, 127].

Колові приклади можуть складати й самі учні.

Відгадування задуманих приладів. На дошці пишуть приклади. Вчитель називає відповідь одного з них (не першого), а учні повинні знайти задуманий учителем приклад за його відповіддю. У цьому разі учні розв’язують усі або майже всі приклади, щоб знайти потрібний. Можна змінити гру: викликати одного учня і повернути його обличчям до класу, а всім учням запропонувати розв’язати в думці («задумати») який-небудь приклад і назвати лише його відповідь; викликаний учень повинен назвати задуманий приклад. Роботу викликаного учня, якщо він розв’язав кілька прикладів, можна оцінити.

Магічні, або цікаві, квадрати. Це квадрати, які складаються з 9, 16, 25 кліток. У клітках мають бути записані такі числа, сума яких у всіх напрямах (рядках, стовпчиках і діагоналях) однакова. В одному випадку всі числа задані - квадрат заповнений (див. перший квадрат). Треба перевірити, чи є квадрат магічним. У другому випадку в квадраті не всі числа задані, але названо суму (див. другий квадрат). Треба заповнити квадрат. У третьому випадку і числа не всі задані і суму не названо, треба ще знайти цю суму і після цього заповнити квадрат (див. третій квадрат).

Сума 15.

Гра, Лото". Цю гру можна використати для закріплення знань табличного множення, а також табличного додавання. Складають картки самі учні під час вивчення і запам’ятовування таблиць множення. До них включають такі табличні результати, які входять до різних таблиць (16, 18, 24, 36), і їх часто учні плутають (54, 56), а також такі, що порівняно важко запам’ятовуються (27, 28, 42, 49, 63, 64, 72, 81).

Після вивчення таблиці множення 4 з усної лічби діти записують у зошитах відповіді прикладів: 2· 8, 9· 2, 4· 6, 3· 9, 4· 9, 4· 8, 4· 7.

Відповіді вчитель перевіряє і записує на дошці, а діти — на раніше приготовлених картках (9 см х 15 см) в різному порядку. Після вивчення таблиці множення 6 додають числа 42, 54, після множення 7 — 49, 63, 56, множення 8 — 64, 72, множення 9 — 81.

Внаслідок такої роботи картка учня матиме вигляд:

Картки інших дітей відрізняються порядком чисел. Вдома кожний учень виготовляє 15 фішок (2 см х 2 см) і нумерує їх від 1 до 15. Під час гри в кожного учня лежить картка і фішки з номерами від 1 до 15. Гру проводять у швидкому темпі. Вчитель називає приклад на табличне множення, діти обчислюють і затуляють фішками відповідні числа на картці. Учні, які добре знають таблицю, швидко затуляють фішками потрібні числа, і на момент закінчення гри будуть добрими обліковцями. Перевірку вчитель може провести в кінці або під час гри. Учитель запитує, яку відповідь дістали в 3, або в 1 або в 12 прикладах, оголошує правильну відповідь і з’ясовує помилки.

Є й інші ігри: «Кращий обліковець», «Сходинка», «Лабіринт», «Математична естафета», відгадування чисел, задуманих дітьми, тощо. Усі вони сприяють розвитку навичок усних обчислень. Вибираючи гру, вчитель повинен керуватися тим, що це не самоціль, що тільки та гра на уроці принесе користь, яка за короткий час дає можливість виконати найбільше число операцій і охопити всіх учнів [20, 33].

Треба систематично перевіряти вміння і навички усних обчислень у дітей. Під час усної лічби вчитель спостерігає за роботою окремих учнів і враховує її, виставляючи поурочний бал. Багато вчителів з метою обліку навичок обчислень успішно використовує математичні диктанти. Для цього підбирають 8−10 завдань різних видів вправ з вивченого матеріалу. На уроці вчитель називає кожне завдання 1−2 рази, а всі учні в звичайних або спеціальних зошитах для усної лічби записують відповіді. Під час перевірки, яку проводять на уроці або після уроків, з’ясовують помилки. Математичний диктант часто використовують для навчання і тренування в обчисленнях, але іноді він може бути контрольним, і тоді роботу кожного учня оцінюють.

Контрольні роботи на перевірку навичок усних обчислень корисно проводити не рідше, як два рази в семестр. Їх проводять у формі математичного диктанту або за варіантами, тексти яких записують на дошці. Зміст контрольних робіт має відповідати програмі і включати раніше вивчений матеріал. Контрольні роботи на усні обчислення треба систематично проводити і в інших класах.

Особливістю усних обчислень є те, що різні види вправ потрібно комплексно використовувати, внаслідок чого в учнів сформуються міцні навички.