Метод Ґаусса-Жордана. 
Метод Гауса

Використовується для розв’язання систем лінійних алгебраїчних рівнянь, знаходження оберненої матриці, знаходження координат вектора у заданому базисі, відшукання рангу матриці. Метод є модифікацією методу Ґаусса. Названий на честь Ґаусса та Жордана.

Алгоритм Обирається перша зліва колонка, що містить хоч одне ненульове значення.

Якщо верхнє число у цій колонці - нуль, то обмінюється увесь перший рядок матриці з іншим рядком матриці, де у цій колонці нема нуля.

Усі елементи першого рядка діляться на верхній елемент обраної колонки.

Від рядків, що залишились, віднімається перший рядок, помножений на перший елемент відповідного рядка, з метою отримання у якості першого елемента кожного рядка (крім першого) нуля.

Далі, повторюємо ці операції із матрицею, отриманою з початкової матриці після викреслювання першого рядка та першого стовпчика.

Після повторення операцій n-1 разів отримаємо верхню трикутну матрицю.

Віднімаємо від передостаннього рядка останній рядок, помножений на відповідний коефіцієнт, щоб у передостанньому рядку залишилась лише 1 на головній діагоналі.

Повторюємо попередній крок для наступних рядків. У результаті отримуємо одиничну матрицю і рішення на місці вільного вектора (над ним необхідно виконувати ті самі перетворення).

Приклад Розв’яжемо систему рівнянь:

Запишемо її у вигляді матриці 3Ч4, де останній рядок є вільним членом:

Виконаємо такі дії:

До рядка 2 додамо: -4 * рядок 1.

До рядка 3 додамо: -9 * рядок 1.

Отримаємо:

До рядка 3 додамо: -3 * рядок 2.

Рядок 2 ділимо на -2.

До рядка 1 додамо: -1 * рядок 3.

До рядка 2 додамо: -3/2 * рядок 3.

До рядка 1 додамо: -1 * рядок 2.

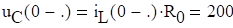
У правому стовпчику отримаємо рішення:

.