Вивчення математичної теми: Піднесення алгебраїчних виразів до степеня

Як приклад наведеної класифікації розглянемо методи цієї класифікації, які використовуються під час вивчення математичної теми: Піднесення алгебраїчних виразів до степеня.

Метод порівняння

Послідовність дій виглядає так: Учні пригадують, що.

52=5*5;

d2=d*d.

Потім ці дії переносять на складніші вирази:

• (a+b)2=(a+b)*(а+b);
• (a-b)2=(a-b)*(a-b).

Учитель лише організовує діяльність учнів.

Метод репродуктивного відтворення та підкріплення

По аналогії з попереднім учні виконують дії:

• (a+b)2=(a+b)-(a+b);
• (a+b)2=a2+ab+ab+b2

і приходять до висновку, що.

• (a+b)2= a2+2ab+b2;
• (a-b)2= a2−2ab-b2;

далі ілюструється один із прикладів застосування отриманої інформації.

472=(50−3)2=502−2*50*3+32=2809.

Метод продуктивного навчання

Учням пропонується завдання типу: піднести до квадрата вираз.

(m-n+c)2.

Можливий хід розв’язку:

(m-n+c)2=[(m-n)+c]2=(m-n)2+ 2(m-n)*c+c2=m2+n2+c2−2(mn+nc-mc).

Інше об'єднання [(m+c)-n]2 дає той же вираз:

• (а+b)3=(а+b)2(а+b)=(a2+2ab+b2)*(a+b);
• (a+b)4=(a+b)2,(a+b)2=(a2+2ab+b2)*(a2+2ab+b2).

Метод творчого засвоєння навчального матеріалу

а) Кодування.

Учням пропонується завдання: Показати достовірність виразу (на рисунку 2).

(a+b)2= a2+2ab+b2.

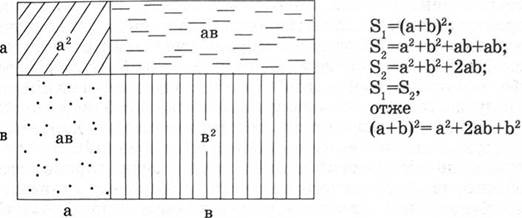
Рис. 2. Геометрична інтерпретація виразу (a+b)2= a2+2ab+b2.

• б) Вивести загальне правило піднесення двочлена до будь-якого степеня:
  • (а+b)2=; (а+b)3=; (а+b)4=; (а+b)5=
• в) Зміна стратегій навчання. Перетворити вираз

a2−2ab+b2;

Учні легко справляються з прямим перетворенням, яке здійснювалось перед цим.

a2-ab-ab+b2=(a2-ab)+(b2-ab)=a (a-b)+b (b-a)=.

=a (a-b)-b (ab)=(a-b)(a-b)=(a-b)2.

Отже (a-b)2=a2−2ab+b2,.

приходять до висновку, що має місце тотожність).