Економетричне моделювання фінансових потоків ПАТ «Приватбанк»

Щоб докладніше дослідити динаміку фінансових потоків нами було проаналізовано показники на присутність регресії, за допомогою програмного продукту Statistica. Було взято основні показники за 2011;2013 роки поквартально та прослідкував їх регресію між собою.

Вихідні данні (млн. грн.) на рис. 3.3.

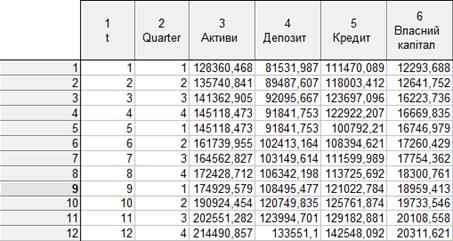
Рис. 3.3 Вихідні данні по балансу ПАТ «Приватбанк»

Та знайшов регресію між кредитом та депозитом с урахуванням змінної t. Це пояснюється тим, що депозити це єдине джерело видачі кредитів. І кількість депозитів безпосередньо впливає на обмеження по кредитах. Основні параметри що необхідні при аналізу моделей регресії показані на рис. 3.4.

Рис. 3.4 Параметри моделі регресії

Як видно з моделі R — коефіцієнт кореляції рівний 0,8394 що говорить про досить високий лінійний зв’язок між залежною змінною — кредитом та незалежними — депозит та t. Коефіцієнт детермінації також досить великий та говорить про те що на 70,473% варіація кредиту пояснюється депозитом та часом. Критерій Фішера показує, що модель адекватна і може використовуватись у прогнозі.

Отримана модель з похибками на рис. 3.5.

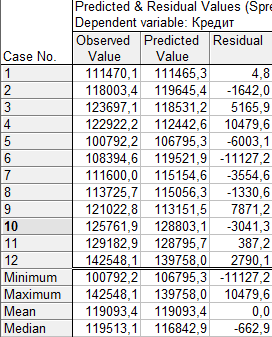
Рис. 3.5 Модель з прогнозними значеннями кредиту та похибками

На рис. 3.6 видно, що змінні t та депозит статистично значимі, та за критерієм Стьюдента видно що гіпотезу можна підтвердити.

Рівняння матиме вигляд лінійного поліному 2-ї ступені:

Y=-24 595,1−5,6473*х1+1,7*х2, (3.1).

Саме це рівняння будемо використовувати в Vensim для підрахунку кредита.

Перевіримо помилки на закон нормального розподілу на графіку на рис. 3.7.

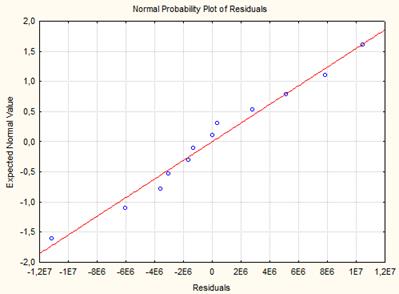
Рис. 3.7 Графік розподілу помилок

Перевіримо помилки на закон нормального розподілу на гістограмі на рис. 3.8.

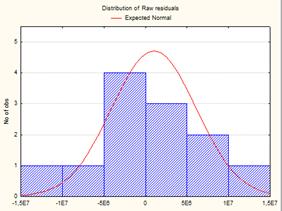
Рис. 3.8 Гістограма розподілу помилок

Помилки розподілені за нормальним законом розподілу.

Знайдемо середню абсолютну процентну похибку на рис. 3.9.

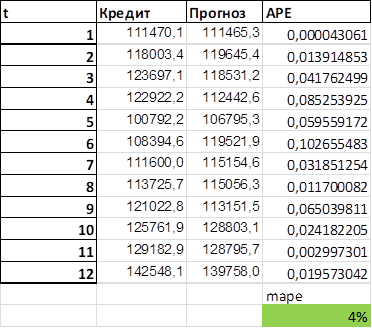
Рис. 3.9 Підрахунок m. a. p. e. в екселі

де APE (абсолютна процентна похибка) — рахується як (Кредит-Прогноз) /Кредит; MAPE — середнє з APE, вона дорівнює 4% що говорить про дуже якісний прогноз та модель.

Кінцева модель для кредиту має вигляд:

Y=-24 595.1−5647.3* (Time+12) +1.7*Deposit, (3.2).

Time — рахується з 1 по 4, тому додаючи 12 отримано прогнозні значення кредиту. Побудуємо модель тренду для власного капіталу, та для знаходження найкращої функції використаємо метод характеристик (повний варіант у додатку В) що показаний у скороченому варіанті на рис. 3.10.

Рис. 3.10. Метод характеристик

Видно з розрахунків що приблизно постійними є показники Tt — 2% та St — 1% варіації, отже тренд цього процесу можна описати такими нелінійними функціями як:

• 1. Показникова функція.
• 2. Степенева функція.

Для вибору остаточного варіанту кривої зростання необхідно зробити розрахунки по обраних кривих і вибрати ту, яка приводить до мінімальних похибок.

Для оцінки параметрів нелінійних моделей використовується процедура лінеаризації, тобто нелінійні моделі приводять шляхом деяких перетворень до лінійного виду, та вже для модифікованих моделей використовується МНК. В табл.3.4 наведені процедури лінеаризації для найбільш типових нелінійних моделей.

Таблиця 3.4. Характеристики, види залежності та процедури лінеаризації.

Характеристика.	Вид залежності.	Процедура лінеаризації.
перші, другі, …, m-ті різниці: ; 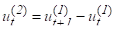; … 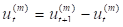.	полиноми відповідно першого, другого, …, m-ого ступеня:	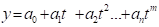заміна, , …, дозволить представити модель у виді:
темпи росту:	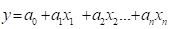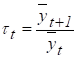показникові функція:	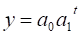логарифмування обох частин рівняння і заміна, ,. дозволить представити модель у виді:
перші різниці зворотних значень рівнів. wt (1) =zt+1-zt	зворотна функція:	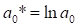заміна дозволить представити модель у виді:
перші прирости логарифмів рівнів.	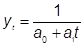степенева (мультиплікативна) функція:	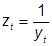логарифмування обох частин рівняння та заміна,, дозволить представити модель у виді:

Розглянемо процедуру лінеаризації для показникової функції.

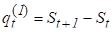
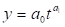
Для лінеаризації застосовуємо процедуру логарифмування:. Робимо заміни:, ,. Отримаємо лінійну форму моделі:. За допомогою аналізу даних зокрема регресії на рис. 3.11. отримуємо а0=9,47 та а1=0,042, по критерію Стьюдента — параметри статистично значимі, тому що t-статистика більше табличного значення, вірогідність помилки статистичної теорії менше ніж 0,05, лінійна форма моделі матиме вигляд:

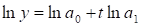
y*=9,47+0,042*t, (3.3).

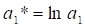
Рис. 3.11. Результати аналізу регресії

Розрахунки показникової моделі показані на рис. 3.12.

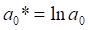
Рис. 3.12. Модель тренду показникової функції

Будуємо прогнозну модель використовуючи знайдені параметри а0 і а1 для тренда і отримуємо середню абсолютну процентну помилку — 5%.

Для того, щоб візуально порівняти вихідні дані та збудований тренд побудований графік на рис. 3.13. з вихідними даними і трендом.

Рис. 3.13. Графік тренду та вихідних даних

Наступним кроком необхідно лінеаризувати степеневу функцію використовуючи таблицю 3.4.

,.

За допомогою вбудованої функції в екселі - аналізу даних регресії, результат можна бачити на рис. 3.14. отримуємо параметри а0=9,39 та а1=0,21, параметри статистично значимі.

Рис. 3.14. Результати аналізу регресії

Розрахунки степеневої моделі показані на рис. 3.15.

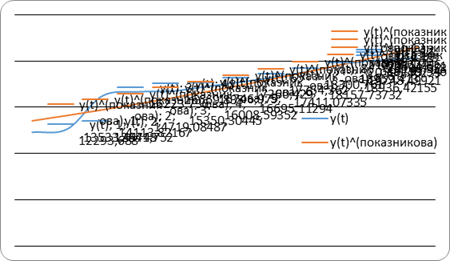
Рис. 3.15. Модель тренду степеневої функції

Mape — усього 3%, різницю між степеневою та показниковою можна побачити на рис. 3.16.

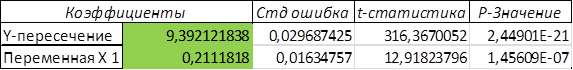
Рис. 3.16. Графік за вихідними даними та моделями тренду степеневої і показникової функцій

Кінцева функція завдання власного капіталу виглядає:

Y=11 993.5* (Time+12)^0.21, (3.4).

де Time — время.

Вона використовується для завдання власного капіталу як додаткову змінну для прогнозування на наступний рік, тому що дотримані два припущення які дозволяють нам використовувати метод екстраполяції:

• 1) часовий ряд економічного показника дійсно має тренд, тобто переважну тенденцію;
• 2) загальні умови, що визначали розвиток показника минулого, залишаться без істотних змін протягом періоду попередження.

Ці рівняння є частиною складної імітаційної моделі. Аналіз регресії показав, що є зв’язок між кредитом та депозитом, тому завдаючи прогноз кредиту на основі депозиту можливо управляти динамікою кредитів через депозити. Для цього необхідно змінювати параметри зняття і поповнення депозитів, і проаналізувавши експерименти прийняти управлінські рішення.