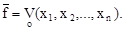Метод простих імлікант

Метод Куайна-Мак-Класкі (метод простих імлікант) — табличний метод мінімізації булевих функцій розроблений Уілардом Куайном і Едвардом Мак-Класкі. Функціонально ідентичний карті Карно, але таблична форма робить його ефективнішим для використання в комп’ютерних алгоритмах.

Незважаючи на більшу можливість практичного застосування ніж у карт Карно, коли мова йде про більше ніж чотири змінних, метод Куайна — Мак-Класкі теж має обмеження області застосування через експоненціальне зростання часу зі збільшенням кількості змінних. Можна показати, що для функції від n змінних верхня границя кількості основних імплікант 3ⁿ/n. Якщо n = 32 їх може бути більше ніж 6.5 * 10¹⁵. Функції з великою кількістю змінних мають бути мінімізовані з допомогою потенційно не оптимального евристичного алгоритму, на сьогодні евристичний алгоритм мінімізації Еспресо є фактичним світовим стандартом.

1-й етап. Знаходження первинних импликант

Всі минтери даної функції порівнюються попарно. Якщо минтерми відрізняються однією координатою типу Fхi + F = F, то виписується кон’юнкція F, що є минтермов (r + l)-гo рангу. Минтерми r-го рангу, для яких відбулося склеювання, відзначаються.

Іншими словами, знаходження простих імплікант зводиться до побудови комплексу кубів.

K (f) = К0 К1 К2… Кr.

При побудові подальших кубів, що утворюють попередні куби відзначаються, щоб виявити невідмічені куби.

Етап закінчується, коли жоден (r +1)-куб не може бути побудований. При цьому, всі невідмічені куби комплексу K (f) теж є простими импликантами і входять у покриття C (f) функції f.

Приклад. Нехай задана функція.

F (х₁, х₂, х₃, х₄, х₅)=(0,1,2,3,4,5,14,15,16,17,18,19,21,23,31).

Прості і невідмічені імпліканти утворюють покриття С (f), яке може бути надмірною і вимагає подальших етапів мінімізації, а саме — складання таблиць покриття функції.

2-й етап. Складання таблиць покриття

Зрозуміло, що для знаходження мінімальної форми покриття необхідно видалити з покриття деякі прості або невідмічені імпліканти. Для цього використовують таблицю, рядки якої складають імпліканти покриття, а стовпці - 0-куби (минтермів) вихідної функції. Якщо імпліканта відрізняється від 0-куба (крім незалежних координат), то на їх перетині не ставиться мітка (див. таблицю 2.1).

Таблиця 2.1-Таблиця покриття комплексу кубів.

3-й етап. Визначення істотних імплікант

Якщо у стовпці таблиці покриттів є тільки одна мітка, то первинна імпліканта, що стоїть у відповідному рядку, є суттєвою імплікантою, і її виписують у нове мінімальне покриття C (f). З таблиці покриттів виключаються рядки, відповідні істотним імплікантам і стовпці мінтермів, вкриває цими істотними імплікантами. Покриття буде мати вигляд:

C (f) = .

В результаті спрощення, отримаємо нову таблицю 2.2.

Таблиця 2.2-Покриття.

4-й етап. Викреслення зайвих стовпців.

Якщо в таблиці істотних імплікант є два стовпці які мають мітки в однакових рядках, то один із стовпців викреслюється.

5-й етап. Викреслення простих зайвих імплікант.

Якщо після викреслювання стовпців в таблиці з’являються рядки без міток, то імпліканти цих рядків викреслюються.

6-й етап. Вибір мінімального покриття.

У таблиці, отриманої після виділення істотних імплікант, вибирається сукупність простих імплікант, що забезпечує покриття всіх стовпців з мінімальною ціною СA.

У нашому прикладі вибирається імпліканта Х0Х01 (або 10ХХ1, тому що ціни СA однакові).

Таким чином, покриття функції має вигляд:

С (f) =.

і визначає мінімальну ДНФ.

f =++x₂x₃x₄+x₅+x₁x₃x₄x₅.

При використанні методу Куайна для ДКНФ необхідно розглядати значення функцій f = 0 і макстерми, відповідні цим значенням. В результаті отримаємо.