Розділ 3. Відкриті і замкнені множини

Деякі поняття теорії метричних просторів

Нехай маємо метричний простір Х, і Е — множина цього простору, х₀Х — точка простору Х.

Означення 1.1. Точка, називається граничною точкою множини Е, якщо в будь-якому околі цієї точки міститься хоча б одна точка множини Е, відмінна від .

Означення 1.2. Точка, називається граничною точкою множини Е, якщо в будь-якому околі цієї точки міститься нескінченна множина точок множини Е.

Означення 1.1 і 1.2 — еквівалентні. Те, що з другого означення випливає перше, очевидно. Покажемо, що з першого означення слідує друге. Доведемо це методом від супротивного! Припустимо, що гранична точка множини Е згідно означення 1.1 і не є граничною згідно означення 1.2. Тоді існує окіл S (x₀;) такий, що в ньому міститься скінченна кількість точок з множини Е. Нехай це будуть точки, причому. Серед чисел, вибираємо найменше. Нехай воно дорівнює r₀. Візьмемо окіл S (x₀;r₀), очевидно. Тоді в околі S (x₀;r₀) нема жодної точки з множини Е, відмінної від. Таким чином ми прийшли до протиріччя.

Означення 1.3. Множину граничних точок множини Е називають похідною множиною множини Е.

Похідну множину позначають .

Теорема 1.1. Для того, щоб точка була граничною точкою множини Е, необхідно і достатньо, щоб існувала збіжна до послідовність попарно різних і відмінних від точок .

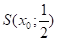
Доведення. Необхідність. Нехай. В кулі існує безліч точок з множини Е. Візьмемо одну з них, яка відмінна від і позначимо її. В кулі також є нескінченна множина точок з Е. Візьмемо одну з них, відмінну від і і позначимо її. Аналогічно з кулі відділяємо точку, яка належить множині Е і відмінна від. Продовжуючи цей процес до нескінченності, одержимо послідовність, , всі різні і. Так, як, коли, то .

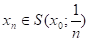
Достатність. Нехай, , коли, і. Тоді для всякого існує натуральне число N таке, що при точки, тобто містяться воколі точки. Отже гранична точка множини Е.

Означення 1.4. Точка, називається точкою дотику множини, якщо в будь-якому околі цієї точки міститься хоча б одна точка з множини Е.

З означення ми бачимо, що точками дотику множини Е є точки самої множини і точки, які є граничними точками для неї.

Означення 1.5. Точка, яка належить множині, але не є граничною для неї, називається ізольованою точкою множини.

Означення 1.6. Точка, називається межовою точкою множини, якщо в будь-якому її околі є точки, які належать даній множині, і точки, які їй не належать.

Означення 1.7. Точка, називається внутрішньою точкою множини, якщо вона належить цій множині разом з деяким своїм околом.